初中数学苏科版七年级下册 7.5 多边形的内角和与外角和同步训练

试卷更新日期：2021-01-14 类型：同步测试

进入出卷网下载

一、单选题

1. 一个多边形外角和是内角和的2倍，这个多边形是（）

A、三角形 B、四边形 C、六边形 D、不能确定

查看试题解析
2. 若一个多边形从一个顶点出发共有7条对角线，则这个多边形的边数为（）

A、8 B、9 C、10 D、11

查看试题解析
3. 在△ABC.若 $∠ A = \frac{1}{2} ∠ B = \frac{1}{3} ∠ C$ ，那么这个三角形是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、以上都不对

查看试题解析
4. 在①正三角形、②正方形、③正六边形中能密铺平面的是（）

A、①②③ B、②③ C、①③ D、以上都不对

查看试题解析
5. 如图，直线a∥b，若∠1＝50°，∠3＝95°，则∠2的度数为（）

A、30° B、40° C、45° D、55°

查看试题解析
6. 如图，在三角形模板ABC中，∠A=60°，D、E分别为AB、AC上的点，则∠1+∠2的度数为（）

A、180° B、200° C、220° D、240°

查看试题解析
7. 如图，AE∥DB ， ∠1＝84°，∠2＝29°，则∠C的度数为（）

A、55° B、56° C、57° D、58°

查看试题解析
8. 如图，在五边形ABCDE中，∠A+∠B+∠E＝300°，DP，CP分别平分∠EDC，∠BCD，则∠P的度数是（　　）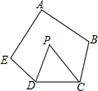

A、60° B、55° C、50° D、45°

查看试题解析
9. 如图： $∠ A + ∠ B + ∠ C + ∠ D + ∠ E + ∠ F$ 等于 $($ $)$

A、 $180^{\circ}$ B、 $360^{\circ}$ C、 $540^{\circ}$ D、 $720^{\circ}$

查看试题解析
10. 如图，∠1、∠2、∠3的大小关系为（）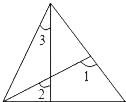

A、∠2＞∠1＞∠3 B、∠1＞∠3＞∠2 C、∠3＞∠2＞∠1 D、∠1＞∠2＞∠3

查看试题解析

二、填空题

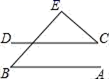
11. 已知一个多边形的每个外角都是24°，此多边形是边形．

查看试题解析
12. 一个多边形的内角和为2700°，则这个多边形的边数是边.

查看试题解析
13. 若一个正多边形的内角是外角的3倍还多20°，则这个多边形的边数是.

查看试题解析
14. 如图，直线AB∥CD，∠B＝50°，∠C＝40°，则∠E等于.

查看试题解析
15. 如图，在△ABC中，点D在AC上，点E在BD上，若∠A=70°，∠ABD=22°，∠DCE=25°，则∠BEC的度数为．

查看试题解析
16. 如图，∠1+∠2+∠3+∠4=度．

查看试题解析
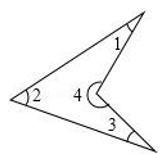17. 如图，小亮从A点出发，沿直线前进15米后向左转30°，再沿直线前进15米，又向左转30°，…照这样走下去，他第一次回到出发地A点时，一共走了米.

查看试题解析
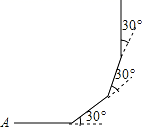18. 一个正三角形和一副三角板（分别含30°和45°）摆放成如图所示的位置，且AB∥CD ．则∠1＋∠2＝．

查看试题解析

三、解答题

19. 将一个凸 $n$ 边形剪去一个角得到一个新的多边形，其内角和为1620°，求 $n$ 的值.

查看试题解析
20. 已知四边形的一个内角是56°，第二个内角是它的2倍，第三个内角比第二个内角小10°．求第四个内角的大小．

查看试题解析

21. 让我们一起来探究“边数大于或等于3的多边形的内角和问题”．

规定：连接多边形不相邻的两个顶点的线段叫做多边形的对角线．

尝试：从多边形某一个顶点出发的对角线可以把一个多边形分成若干个三角形，这样，就把“多边形内角和问题”转化为“三角形内角和问题”了．

(1)、请你在下面表格中，试一试，做一做，并将表格补充完整：

名称	图形	内角和
三角形		180°
四边形		2 ×180°=360°
五边形
六边形

(2)、根据上面的表格，请你猜一猜，七边形的内角和等于；如果一个多边形有n条边，请你用含有n的代数式表示这个多边形的内角和．

(3)、如果一个多边形的内角和是1260°，请判断这个多边形是几边形．

查看试题解析

22. 如图，点D、B、C在同一条直线上，∠A=60°，∠C=50°，∠D=25°.求∠1的度数.

查看试题解析
23. 如图所示，在△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC=50°，∠C=70°，求∠DAC、∠BOA的度数．

查看试题解析
24. 如图，求∠A+∠B+∠C+∠D+∠E的大小．

查看试题解析
25.

(1)、如图①，AB∥CD，如果∠BAE=60°，∠ECD=45，求∠AEC的度数请将下面的求解过程填写完整．

解：过点E画直线EF，使EF∥AB．

因为EF∥AB，根据“”，可得∠BAE=∠1．又因为∠BAE=60°，所以∠1=°．因为EF∥AB，且AB∥CD，根据“”，可得EF∥CD所以∠ECD=∠ ．又因为∠ECD=45°，所以，所以∠AEC=°．

(2)、如图②，AB∥CD，如果∠BAE=120°，∠ECD=140°，请问∠AEC等于多少度？写出求解过程．

(3)、填空：如图③，AB∥CD，请用一个等式表示∠BAE、∠AEC与∠ECD三个角之间的关系：．

查看试题解析
26. 阅读理解：请你参与下面探究过程，完成所提出的问题.

(1)、问题引入：
如图①，在 $Δ A B C$ 中，点 $O$ 是 $∠ A B C$ 和 $∠ A C B$ 平分线的交点，若 $∠ A = 70^{°}$ ，则 $∠ B O C =$ 度；若 $∠ A = α$ ，则 $∠ B O C =$ （用含 $α$ 的代数式表示）；

(2)、类比探究：
如图②，在 $Δ A B C$ 中， $∠ C B O = \frac{1}{3} ∠ A B C$ ， $∠ B C O = \frac{1}{3} ∠ A C B$ ， $∠ A = α$ .试探究： $∠ B O C$ 与 $∠ A$ 的数量关系（用含 $α$ 的代数式表示），并说明理由.

(3)、知识拓展：
如图③， $B O$ 、 $C O$ 分别是 $Δ A B C$ 的外角 $∠ D B C$ ， $∠ E C B$ 的 $n$ 等分线，它们的交于点 $O$ ， $∠ C B O = \frac{1}{n} ∠ E C B$ ， $∠ B C O = \frac{1}{n} ∠ E C B$ ， $∠ A = α$ ，求 $∠ B O C$ 的度数（用含 $α$ 、 $n$ 的代数式表示）.

查看试题解析

初中数学苏科版七年级下册 7.5 多边形的内角和与外角和 同步训练

一、单选题

二、填空题

三、解答题

初中数学苏科版七年级下册 7.5 多边形的内角和与外角和同步训练