初中数学苏科版七年级下册 7.4 认识三角形 同步训练
试卷更新日期:2021-01-13 类型:同步测试
一、单选题
-
1. 下列哪些线段能组成三角形( )
①3cm、3cm、5cm ②3cm、3cm、3cm ③2cm、2cm、4cm ④3cm、5cm、9cm
A、①② B、③④ C、①②③ D、①②③④2. 能将一个三角形分成面积相等的两个三角形的一条线段是( )A、三角形的高线 B、边的中垂线 C、三角形的中线 D、三角形的角平分线3. 在下列各图的△ABC中,正确画出AC边上的高的图形是( )A、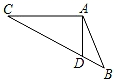 B、
B、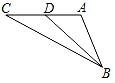 C、
C、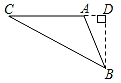 D、
D、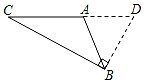 4. 下列说法错误的是( )A、任意三角形都有三条高线、中线、角平分线 B、钝角三角形有两条高线在三角形的外部 C、直角三角形只有一条高线 D、锐角三角形的三条高线、三条中线、三条角平分线分别交于一点5. 如图,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D、C、F,下列说法中,不正确的是( )
4. 下列说法错误的是( )A、任意三角形都有三条高线、中线、角平分线 B、钝角三角形有两条高线在三角形的外部 C、直角三角形只有一条高线 D、锐角三角形的三条高线、三条中线、三条角平分线分别交于一点5. 如图,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D、C、F,下列说法中,不正确的是( )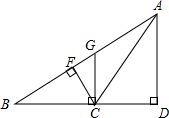 A、△ABC中,AD是边BC上的高 B、△ABC中,GC是边BC上的高 C、△GBC中,GC是边BC上的高 D、△GBC中,CF是边BG上的高6. 如图,D是△ABC的边BC上任意一点,E、F分别是线段AD.CE的中点,且△ABC的面积为20cm2 , 则△BEF的面积是( )
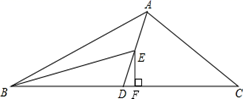
A、△ABC中,AD是边BC上的高 B、△ABC中,GC是边BC上的高 C、△GBC中,GC是边BC上的高 D、△GBC中,CF是边BG上的高6. 如图,D是△ABC的边BC上任意一点,E、F分别是线段AD.CE的中点,且△ABC的面积为20cm2 , 则△BEF的面积是( )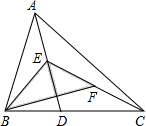 A、10 B、9 C、6 D、57. 如图,点 在直线 上移动, 是直线 上的两个定点,且直线 .对于下列各值:①点 到直线 的距离;② 的周长;③ 的面积;④ 的大小.其中不会随点 的移动而变化的是( )
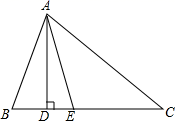
A、10 B、9 C、6 D、57. 如图,点 在直线 上移动, 是直线 上的两个定点,且直线 .对于下列各值:①点 到直线 的距离;② 的周长;③ 的面积;④ 的大小.其中不会随点 的移动而变化的是( )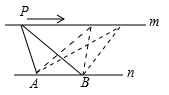 A、①② B、①③ C、②④ D、③④8. a,b,c为△ABC的三边,化简|a+b+c|-|a-b-c|-|a-b+c|-|a+b-c|,结果是( )A、0 B、2a+2b+2c C、4a D、2b2c9. 如图,AE是△ABC的角平分线,AD⊥BC于点D,点F为BC的中点,若∠BAC=104°,∠C=40°,则有下列结论:①∠BAE=52°;②∠DAE=2°;③EF=ED;④S△ABF= S△ABC.其中正确的个数有( )
A、①② B、①③ C、②④ D、③④8. a,b,c为△ABC的三边,化简|a+b+c|-|a-b-c|-|a-b+c|-|a+b-c|,结果是( )A、0 B、2a+2b+2c C、4a D、2b2c9. 如图,AE是△ABC的角平分线,AD⊥BC于点D,点F为BC的中点,若∠BAC=104°,∠C=40°,则有下列结论:①∠BAE=52°;②∠DAE=2°;③EF=ED;④S△ABF= S△ABC.其中正确的个数有( )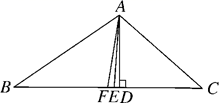 A、1个 B、2个 C、3个 D、4个10. 设△ABC的面积为1,如图①将边BC、AC分别2等份,BE1、AD1相交于点O,△AOB的面积记为S1;如图②将边BC、AC分别3等份,BE1、AD1相交于点O,△AOB的面积记为S2;……, 依此类推,则S5的值为( )
A、1个 B、2个 C、3个 D、4个10. 设△ABC的面积为1,如图①将边BC、AC分别2等份,BE1、AD1相交于点O,△AOB的面积记为S1;如图②将边BC、AC分别3等份,BE1、AD1相交于点O,△AOB的面积记为S2;……, 依此类推,则S5的值为( )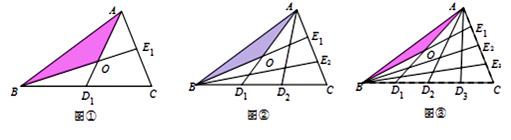 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在门框钉一根木条能固定住门框,不易变形,这里利用的数学原理是 .12. 从长为3 cm,5cm,7cm,10cm的四根木棒中选出三根组成三角形,共有种选法.13. 若H是△ABC三条高AD、BE、CF的交点,则△HBC中BC边上的高是 , △BHA中BH边上的高是 .
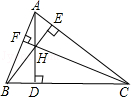 14. 如图,已知AE是△ABC的边BC上的中线,若AB=8cm,△ACE的周长比△AEB的周长多2cm,则AC=cm.
14. 如图,已知AE是△ABC的边BC上的中线,若AB=8cm,△ACE的周长比△AEB的周长多2cm,则AC=cm.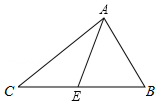 15. 如图, AD//BC, BD、AC 相交于点 O, △AOB 的面积为 2, △BOC 的面积为 4,则△DOC 的面积等于 .
15. 如图, AD//BC, BD、AC 相交于点 O, △AOB 的面积为 2, △BOC 的面积为 4,则△DOC 的面积等于 .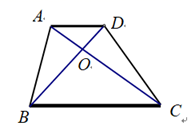 16. △ABC中,AB=AC,一腰上的中线BD把三角形的周长分为9cm和12cm两部分,则此三角形的腰长是 .17. 如图,△ABC的面积为49cm2 , AE=ED,BD=3DC,则图中△AEF的面积等于.
16. △ABC中,AB=AC,一腰上的中线BD把三角形的周长分为9cm和12cm两部分,则此三角形的腰长是 .17. 如图,△ABC的面积为49cm2 , AE=ED,BD=3DC,则图中△AEF的面积等于.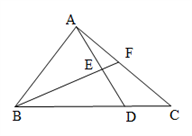 18. 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为4、5、7,四边形DHOG面积为.
18. 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为4、5、7,四边形DHOG面积为.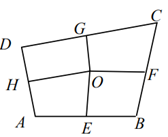
三、解答题
-
19. 如图,△ABC,按要求完成下列各题:
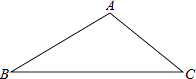
①画△ABC的中线CD;
②画△ABC的角平分线AE;
③画△ABC的高BF;
④画出把△ABC沿射线BF方向平移3cm后得到的△A1B1C1 .
20. 如图,在△ABC中,点D、E分别为BC、AD的中点,若S△ABC=1,求S△ABE . 21. 如图,已知△ABC的高AD,角平分线AE,∠B=26°,∠ACD=56°,求∠AED的度数。
21. 如图,已知△ABC的高AD,角平分线AE,∠B=26°,∠ACD=56°,求∠AED的度数。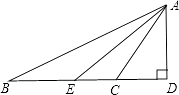 22. 在锐角三角形ABC中,AB>AC,AM为中线,P为△AMC内一点,证明:PB>PC(如图).
22. 在锐角三角形ABC中,AB>AC,AM为中线,P为△AMC内一点,证明:PB>PC(如图).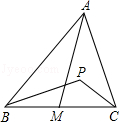 23. 如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.
23. 如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.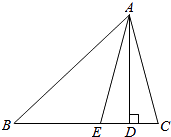 24. 如图,AD、CE是△ABC的两条高,已知AD=10,CE=9,AB=12.
24. 如图,AD、CE是△ABC的两条高,已知AD=10,CE=9,AB=12.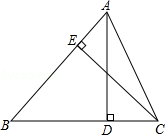 (1)、求△ABC的面积;(2)、求BC的长.
(1)、求△ABC的面积;(2)、求BC的长.