湖北省武汉市同济附中2020-2021学年七年级上学期数学期末考试卷

试卷更新日期：2021-01-13 类型：期末考试

进入出卷网下载

一、单选题

1. -2的倒数是（）

A、2 B、-2 C、0 D、 $- \frac{1}{2}$

查看试题解析
2. 下列计算：① $0 - (- 2) = - 2$ ；② $(- 5) + (- 6) = - 11$ ；③ $\frac{4}{9} \times (- \frac{3}{2}) = - \frac{2}{3}$ ；④ $(- 56) \div (- 8) = - 7$ .其中正确的有（）

A、①② B、②③ C、③④ D、②④

查看试题解析
3. 冥王星围绕太阳公转的轨道半径长度约为5900000000千米，5900000000用科学记数法表示是（）

A、5.9×10¹⁰ B、5.9×10⁹ C、59×10⁸ D、0.59×10¹⁰

查看试题解析
4. 一个三角形的三边之比为2∶3∶3，最短边为6，则这个三角形的周长为（）

A、32 B、24 C、25 D、36

查看试题解析
5. 小刚学习了有理数运算法则后，编了一个计算程序，当他输入任意一个有理数时，显示屏上出现的结果总等于所输入的有理数的平方与1的和，当他第一次输入2，然后将所得到的结果再次输入后，显示屏上出现的结果应是（）

A、－8 B、5 C、－24 D、26

查看试题解析
6. 一块地有a公顷，平均每公顷产粮食m千克；另一块地有b公顷，平均每公顷产粮食n 千克，则这两块地平均每公顷的粮食产量为（）

A、 $\frac{m + n}{2}$ B、 $\frac{a + b}{2}$ C、 $\frac{a m + b n}{a + b}$ D、 $\frac{a m + b n}{m + n}$

查看试题解析
7. 下列各题正确的是（）

A、由 $7 x = 4 x - 3$ 移项得 $7 x - 4 x = 3$ B、由 $\frac{2 x - 1}{3} = 1 + \frac{x - 3}{2}$ 去分母得 $2 (2 x - 1) = 1 + 3 (x - 3)$ C、由 $2 (2 x - 1) - 3 (x - 3) = 1$ 去括号得 $4 x - 2 - 3 x - 9 = 1$ D、由 $2 (x + 1) = x + 7$ 去括号、移项、合并同类项得 $x = 5$

查看试题解析
8. 观察下列等式： $3^{1} = 3$ ， $3^{2} = 9$ ， $3^{3} = 27$ ， $3^{4} = 81$ ， $3^{5} = 243$ ， $3^{6} = 729$ ，……，通过观察，找出规律，确定 $3^{2021}$ 的个位数字是（）

A、3 B、9 C、7 D、1

查看试题解析
9. 如图，数轴上每相邻两点相距一个单位长度，点A、B、C、D对应的位置如图所示，它们对应的数分别是a、b、c、d，且d﹣b+c=10，那么点A对应的数是（）

A、﹣6 B、﹣3 C、0 D、正数

查看试题解析
10. 把几个不同的数用大括号括起来，相邻两个数之间用逗号隔开，如：{1，2}；{1，4，7}；我们称之为集合，其中的每一个数称为该集合的元素.规定：当整数x是集合的一个元素时，100－x也必是这个集合的元素，这样的集合又称为黄金集合，例如{－1，101}就是一个黄金集合.若一个黄金集合所有元素之和为整数m，且1180＜m＜1260，则该黄金集的元素的个数是（）

A、23 B、24 C、24或25 D、26

查看试题解析

二、填空题

11. 计算： $- 2^{2} - 1 =$ .

查看试题解析
12. $70 ° 1 5^{'} =$ °.

查看试题解析
13. 如果|2x+5|=3，则 x=.

查看试题解析
14. 若m、n互为倒数，则 $m n^{2} - (n + 3)$ 的值为.

查看试题解析
15. 已知等式 $a (2 x + 1) = 3 x - \frac{b}{2}$ ,无论x取何值等式都成立,则 $a b =$ .

查看试题解析
16. 如图，点C、D分别为线段 $A B$ （端点A、B除外）上的两个不同的动点，点D始终在点C右侧，图中所有线段的和等于40cm，且 $A B = 3 C D$ ，则 $C D =$ cm.

查看试题解析

三、解答题

17. 计算：

(1)、 $2 - (- 8) + (- 3) - 5$ ；

(2)、 ${(- 2)}^{2} \div \frac{1}{5} + {(- 2)}^{3} \times \frac{1}{4}$ .

查看试题解析
18. 化简求值： $(3 a - 4 a^{2} + 1 + 2 a^{3}) - (- a + 5 a^{2} + 3 a^{3})$ ，其中 $a = - 1$ .

查看试题解析
19. 解方程：

(1)、 $4 x - 1 = 3 + 2 x$ ；

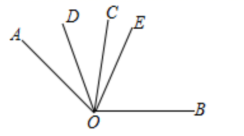
(2)、 $\frac{x + 1}{2} - 2 = 1 + \frac{2 - x}{4}$ .

查看试题解析
20. 一个角的余角比它的补角的 $\frac{1}{4}$ 大15°，求这个角的度数．

查看试题解析
21. 一架飞机飞行在两个城市之间，顺风要2小时45分钟，逆风要3小时，已如风速是每小时24千米，则两城市间的距离为多少？

查看试题解析
22. 如图， $O E$ 平分 $∠ A O B$ ， $O D$ 平分 $∠ A O C$ ， $∠ D O E = 40 °$ ，求 $∠ B O C$ 的度数.

查看试题解析

23. 下表中有两种移动电话计费方式：

	月使用费(元)	主叫限定时间(分钟)	主叫超时费(元/分钟)	被叫
方式一	65	160	0.25	免费
方式二	100	380	0.19	免费

说明：月使用费固定收取，主叫不超限定时间不再收费，主叫超时部分加收超时费；被叫免费.

(1)、若李杰某月主叫通话时间为200分钟则他按方式一计费需元，按方式二计费需元；若他按方式二计费需103.8元，则主叫通话时间为分钟；

(2)、是否存在某主叫通话时间t(分钟)，按方式一和方式二的计费相等，若存在，请求出t的值；若不存在，请说明理由；

(3)、请你通过计算分析后，直接给出当月主叫通话时间t(分钟)满足什么条件时，选择方式一省钱；当每月主叫通话时间t(分钟)满足什么条件时，选择方式二省钱.

查看试题解析

24. 已知，C为线段 $A B$ 上一点，D为 $A C$ 的中点，E为 $B C$ 的中点，F为 $D E$ 的中点.

(1)、如图1，若 $A C = 4$ ， $B C = 6$ ，求 $C F$ 的长；

(2)、若 $A B = 16 C F$ ，求 $\frac{A C}{C B}$ 的值；

(3)、若 $A C > B C$ ， $A C - B C = a$ ，取 $D C$ 的中点 $D_{1}$ ， $CE$ 的中点 $E_{1}$ ， $D_{1} E_{1}$ 的中点 $F_{1}$ ，则 ${CF}_{1}$ =（用含a的代数式表示）.

查看试题解析