辽宁省鞍山市岫岩县2021届九年级上学期数学12月月考试卷
试卷更新日期:2021-01-13 类型:月考试卷
一、单选题
-
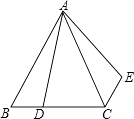
1. 若关于x的方程 有一个根为-2,则a的值是( )A、4 B、-2 C、-3 D、-42. 将二次函数 的图象向上平移3个单位长度,再向左平移2个单位长度,得到的抛物线相应的函数表达式为( )A、 B、 C、 D、3. 如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,△ABD经旋转后到达△ACE的位置,那么旋转了( )
 A、75° B、45° C、60° D、15°4. 关于二次函数 的下列结论,不正确的是( )A、图象的开口向上 B、当 时,y随x的增大而减小 C、图象经过点 D、图象的对称轴是直线5. 一个正多边形绕它的中心旋转45°后,就与原正多边形第一次重合,那么这个正多边形( )A、是轴对称图形,但不是中心对称图形 B、是中心对称图形,但不是轴对称图形 C、既是轴对称图形,又是中心对称图形 D、既不是轴对称图形,也不是中心对称图形6. 如图, 的顶点A在反比例函数 的图象上,顶点C在x轴上, 轴,若点B的坐标为 , ,则k的值为( )
A、75° B、45° C、60° D、15°4. 关于二次函数 的下列结论,不正确的是( )A、图象的开口向上 B、当 时,y随x的增大而减小 C、图象经过点 D、图象的对称轴是直线5. 一个正多边形绕它的中心旋转45°后,就与原正多边形第一次重合,那么这个正多边形( )A、是轴对称图形,但不是中心对称图形 B、是中心对称图形,但不是轴对称图形 C、既是轴对称图形,又是中心对称图形 D、既不是轴对称图形,也不是中心对称图形6. 如图, 的顶点A在反比例函数 的图象上,顶点C在x轴上, 轴,若点B的坐标为 , ,则k的值为( )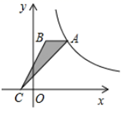 A、4 B、-4 C、7 D、-77. 如图,在⊙O中,点B是 的中点,点 在 上,连接 、 、 、 .若 ,则 的大小为( )
A、4 B、-4 C、7 D、-77. 如图,在⊙O中,点B是 的中点,点 在 上,连接 、 、 、 .若 ,则 的大小为( )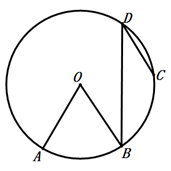 A、50° B、350° C、25° D、150°8. 如图,在平面直角坐标系中,正方形 的顶点O与坐标原点重合,顶点A、C分别在x轴、y轴上,反比例函数 的图象与正方形 的两边 、 分别交于点M、N, 轴,垂足为D,连接 、 、 ,下列结论错误的是① ;②四边形 与 面积相等;③ ;④若 , ,则点C的坐标为 .其中正确的结论有( )
A、50° B、350° C、25° D、150°8. 如图,在平面直角坐标系中,正方形 的顶点O与坐标原点重合,顶点A、C分别在x轴、y轴上,反比例函数 的图象与正方形 的两边 、 分别交于点M、N, 轴,垂足为D,连接 、 、 ,下列结论错误的是① ;②四边形 与 面积相等;③ ;④若 , ,则点C的坐标为 .其中正确的结论有( )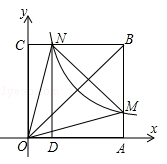 A、①② B、①②④ C、②③④ D、①②③④
A、①② B、①②④ C、②③④ D、①②③④二、填空题
-
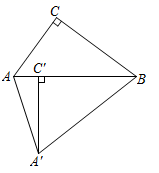
9. 已知点 在反比例函数 上的图象上,则k的值为.10. 抛物线 的顶点坐标为.11. 我国快递业务逐年增加,2017年至2019年快递业务收入由5000亿元增加到7500亿元.设2017年至2019年快递业务收入的年平均增长率为x,则可列方程为.12. 如图, 中, , .将 绕点B逆时针旋转得到 ,点C的对应点C'落在 边上, ,连接 .则 长为.
 13. 如图,在矩形ABCD中,AB=6,AD=8,以顶点A为圆心作半径为r的圆,若要求另外三个顶点至少有一个在圆内,且至少有一个在圆外,则r的取值范围是.
13. 如图,在矩形ABCD中,AB=6,AD=8,以顶点A为圆心作半径为r的圆,若要求另外三个顶点至少有一个在圆内,且至少有一个在圆外,则r的取值范围是.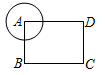 14. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,该圆锥的母线长 ,则扇形的圆心角 度数为.
14. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径 ,该圆锥的母线长 ,则扇形的圆心角 度数为.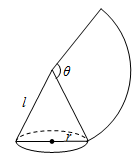 15. 二次函数 的部分图象如图所示,对称轴为直线 ,则关于x的方程 的解为.
15. 二次函数 的部分图象如图所示,对称轴为直线 ,则关于x的方程 的解为.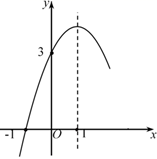 16. 如图,在直角坐标系中,四边形 是正方形,点A的坐标为 ,点B的坐标为 .若正方形 和正方形 关于点 成中心对称:正方形 和正方形 关于点 成中心对称;…,依此规律,则点 的坐标为.
16. 如图,在直角坐标系中,四边形 是正方形,点A的坐标为 ,点B的坐标为 .若正方形 和正方形 关于点 成中心对称:正方形 和正方形 关于点 成中心对称;…,依此规律,则点 的坐标为.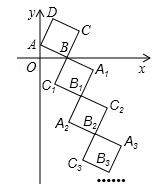
三、解答题
-
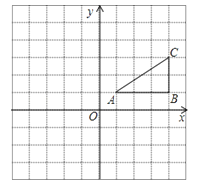
17. 用适当方法解方程:18. 如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).
(1)先将Rt△ABC向左平移5个单位长度,再向下平移1个单位长度得到Rt△A1B1C1 , 试在图中画出Rt△A1B1C1 , 并写出点A1的坐标;
(2)再将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2 , 试在图中画出Rt△A2B2C2 , 并计算Rt△A1B1C1在上述旋转过程中点C1所经过的路径长.
 19. 关于x的一元二次方程 有两个不相等的实数根.(1)、求m的取值范围;(2)、设出 、 是方程的两根,且 ,求 的值.20. 尊老爱幼是中华民族的传统美德,九九重阳节前夕,某商店为老人推出一款特价商品,每件商品的进价为15元,促销前销售单价为25元,平均每天能售出80件;根据市场调查,销售单价每降低0.5元,平均每天可多售出20件.(1)、若每件商品降价5元,则商店每天的平均销量是件(直接填写结果);(2)、不考虑其他因素的影响,若商店销售这款商品的利润要平均每天达到1280元,每件商品的定价应为多少元?(列方程求解)21. 如图,已知 是 的直径,C,D是 上的点, ,交 于点E,连结 .
19. 关于x的一元二次方程 有两个不相等的实数根.(1)、求m的取值范围;(2)、设出 、 是方程的两根,且 ,求 的值.20. 尊老爱幼是中华民族的传统美德,九九重阳节前夕,某商店为老人推出一款特价商品,每件商品的进价为15元,促销前销售单价为25元,平均每天能售出80件;根据市场调查,销售单价每降低0.5元,平均每天可多售出20件.(1)、若每件商品降价5元,则商店每天的平均销量是件(直接填写结果);(2)、不考虑其他因素的影响,若商店销售这款商品的利润要平均每天达到1280元,每件商品的定价应为多少元?(列方程求解)21. 如图,已知 是 的直径,C,D是 上的点, ,交 于点E,连结 .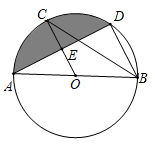 (1)、求证: ;(2)、若 , ,求图中阴影部分的面积.22. 已知反比例函数 与一次函数 的图象相交于点 ,和点 .
(1)、求证: ;(2)、若 , ,求图中阴影部分的面积.22. 已知反比例函数 与一次函数 的图象相交于点 ,和点 .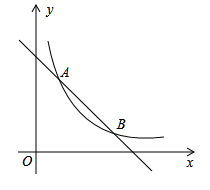 (1)、求反比例函数与一次函数的解析式;(2)、求出 的面积;(3)、直接写出不等式 的解集.23. 如图,在 中, , 平分 ,交 于点O,以O为圆心, 为半径作圆,交 于点E.
(1)、求反比例函数与一次函数的解析式;(2)、求出 的面积;(3)、直接写出不等式 的解集.23. 如图,在 中, , 平分 ,交 于点O,以O为圆心, 为半径作圆,交 于点E. (1)、求证: 与 相切.(2)、连接 并延长,交 于点F,若 ,且 ,求 的半径.24. 某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他各项费用80元.
(1)、求证: 与 相切.(2)、连接 并延长,交 于点F,若 ,且 ,求 的半径.24. 某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他各项费用80元.销售单价x(元)
3.5
5.5
销售量y(袋)
280
120
(1)、请直接写出y与x之间的函数关系式;(2)、如果每天获得160元的利润,销售单价为多少元?(3)、设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?25. 如图1、2是两个斜边比为 的等腰直角三角形,将两个三角形如图3放置,小直角三角形的斜边与大直角三角形的一直角边重合.
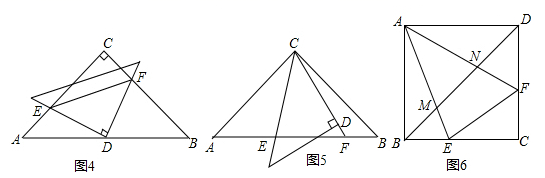 (1)、在图3中,绕点D旋转小直角三角形,使两直角边分别与 、 交于点E,F,如图4,请直接写出 , , 之间的关系:;(2)、若在图3中,绕点C旋转小直角三角形,使它的斜边和 延长线分别与 交于点E,F,如图5,此时(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)、如图6,在正方形 中,E、F分别是边 、 上的点,满足 的周长等于正方形 的周长的一半, 、 分别与对角线 交于M、N,试问线段 、 、 能否构成三角形的三边长?若能,指出三角形的形状,并给出证明;若不能,请说明理由.26. 如图,已知抛物线 与x轴相交于 , 两点,与y轴相交于点 ,抛物线的顶点为D.
(1)、在图3中,绕点D旋转小直角三角形,使两直角边分别与 、 交于点E,F,如图4,请直接写出 , , 之间的关系:;(2)、若在图3中,绕点C旋转小直角三角形,使它的斜边和 延长线分别与 交于点E,F,如图5,此时(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)、如图6,在正方形 中,E、F分别是边 、 上的点,满足 的周长等于正方形 的周长的一半, 、 分别与对角线 交于M、N,试问线段 、 、 能否构成三角形的三边长?若能,指出三角形的形状,并给出证明;若不能,请说明理由.26. 如图,已知抛物线 与x轴相交于 , 两点,与y轴相交于点 ,抛物线的顶点为D.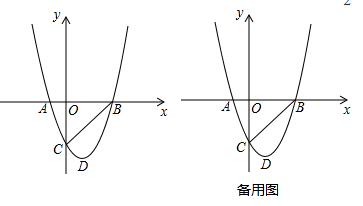 (1)、求抛物线的解析式;(2)、若点E在x轴上,且在点B左侧、 ,求点 E的坐标.(3)、若P是直线 下方抛物线上任意一点,过点P作 轴于点 H,与 交于点M.
(1)、求抛物线的解析式;(2)、若点E在x轴上,且在点B左侧、 ,求点 E的坐标.(3)、若P是直线 下方抛物线上任意一点,过点P作 轴于点 H,与 交于点M.①求线段 长度的最大值.
②在①的条件下,若F为y轴上一动点,求 的最小值.