浙江省台州市仙居县2021届九年级数学上学期数学期末考试卷
试卷更新日期:2021-01-13 类型:期末考试
一、单选题
-
1. 下列四个标志中.既是轴对称图形又是中心对称图形的是( )A、
 B、
B、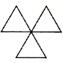 C、
C、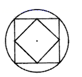 D、
D、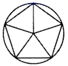 2. 下列语句中描述的事件必然发生的是( )A、15个人中至少有两个人同月出生 B、一位同学在打篮球,投篮一次就投中 C、在1,2,3,4中任取两个数,它们的和大于7 D、掷一枚硬币,正面朝上3. 如图,四边形 是 的内接四边形, ,则 的度数为( )
2. 下列语句中描述的事件必然发生的是( )A、15个人中至少有两个人同月出生 B、一位同学在打篮球,投篮一次就投中 C、在1,2,3,4中任取两个数,它们的和大于7 D、掷一枚硬币,正面朝上3. 如图,四边形 是 的内接四边形, ,则 的度数为( ) A、70° B、90° C、100° D、110°4. 一只不透明的袋子里放着6个只有颜色不同的小球,其中4个白球、2个红球,从该袋子里摸出一个球,摸到的球是红球的概率是( )A、 B、 C、 D、5. 将函数 的图象向右平移2个单位.再向下平移4个单位.所得图象的对称轴是( )A、 B、 C、 D、6. 用配方法解一元二次方程 ,下列变形中正确的是( )A、 B、 C、 D、7. 某商场销售一批衬衣.平均每天可售出30件.每件衬衣盈利50元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衣降价10元,商场平均每天可多售出20件.若商场平均每天盈利2000元.每件衬衣应降价( )元.A、10 B、15 C、20 D、258. 正六边形的边长为 ,则它的面积为( )A、 B、 C、 D、9. 如图, 为 的直径,点 是弧 的中点.过点 作 于点 ,交 于点 ,若 , ,则 的半径长是( )
A、70° B、90° C、100° D、110°4. 一只不透明的袋子里放着6个只有颜色不同的小球,其中4个白球、2个红球,从该袋子里摸出一个球,摸到的球是红球的概率是( )A、 B、 C、 D、5. 将函数 的图象向右平移2个单位.再向下平移4个单位.所得图象的对称轴是( )A、 B、 C、 D、6. 用配方法解一元二次方程 ,下列变形中正确的是( )A、 B、 C、 D、7. 某商场销售一批衬衣.平均每天可售出30件.每件衬衣盈利50元.为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衣降价10元,商场平均每天可多售出20件.若商场平均每天盈利2000元.每件衬衣应降价( )元.A、10 B、15 C、20 D、258. 正六边形的边长为 ,则它的面积为( )A、 B、 C、 D、9. 如图, 为 的直径,点 是弧 的中点.过点 作 于点 ,交 于点 ,若 , ,则 的半径长是( ) A、5 B、6.5 C、7.5 D、810. 已知两个整数 , ,有 ,则 的最大值是( )A、35 B、40 C、41 D、42
A、5 B、6.5 C、7.5 D、810. 已知两个整数 , ,有 ,则 的最大值是( )A、35 B、40 C、41 D、42二、填空题
-
11. 关于 的一元二次方程 的一个根为1,则 .12. 某商场设立了一个可以自由转动的转盘,并规定:顾客购物30元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
转动转盘的次数
100
200
300
500
1000
落在“签字笔”区域的次数
65
122
190
306
601
假如你去转动该转盘一次.你获得签字笔的概率约是.(精确到0.1)
13. 如图,已知点 , , , ,连接 , ,将线段 绕着某一点旋转一定角度,使 , 分别与 , 重合,则旋转中心的坐标为.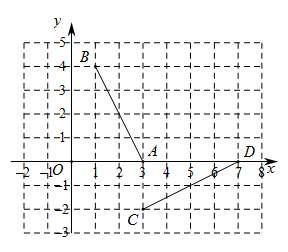 14. 如图,一把折扇展开后的圆心角为120°,扇骨 长为 ,扇面宽 ,则该折扇的扇面的面积 .
14. 如图,一把折扇展开后的圆心角为120°,扇骨 长为 ,扇面宽 ,则该折扇的扇面的面积 . 15. 已知二次函数 的图象上有 , , 三个点.用“<”连接 , , 的结果是.16. 一种圆角正方形桌面如图所示.每段圆弧所对的圆心角是90°,用一根直尺测得轮廓上两点之间距离的最大值是 ,平行的两直边之间的距离为 ,则该圆角正方形的周长是.
15. 已知二次函数 的图象上有 , , 三个点.用“<”连接 , , 的结果是.16. 一种圆角正方形桌面如图所示.每段圆弧所对的圆心角是90°,用一根直尺测得轮廓上两点之间距离的最大值是 ,平行的两直边之间的距离为 ,则该圆角正方形的周长是.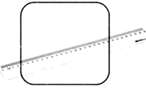
三、解答题
-
17. 解下列方程:(1)、 ;(2)、 .18. 学校食堂每天中午为学生提供 , , 三种不同套餐.用列举法分析甲乙两人选择同款套餐的概率.19. 如图,边长为1的正方形组成的网格中, 的顶点均在格点上.点 , , 的坐标分别是 , , .
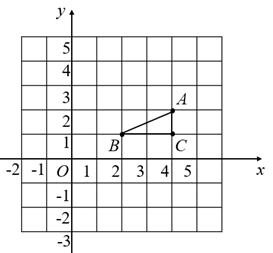 (1)、作出 绕点 顺时针旋转90°以后的图形.写出旋转后点 对应点的坐标;(2)、求点 在旋转过程中所经过路径的长度.20. 已知:抛物线 与直线 交于 , 两点.(1)、求抛物线顶点 的坐标;(2)、当 取何值时, 成立.21. 背景:用圆规和没有刻度的直尺作图具有以下基本事实保证:已知圆心和半径能作一个圆且只能作一个圆;经过两点能作且只能作一条直线.尺规作图的原理是:通过圆、直线相交作出点,连接两点作线段,并进一步由线段组成各种图形.
(1)、作出 绕点 顺时针旋转90°以后的图形.写出旋转后点 对应点的坐标;(2)、求点 在旋转过程中所经过路径的长度.20. 已知:抛物线 与直线 交于 , 两点.(1)、求抛物线顶点 的坐标;(2)、当 取何值时, 成立.21. 背景:用圆规和没有刻度的直尺作图具有以下基本事实保证:已知圆心和半径能作一个圆且只能作一个圆;经过两点能作且只能作一条直线.尺规作图的原理是:通过圆、直线相交作出点,连接两点作线段,并进一步由线段组成各种图形.问题:已知圆心 和半径 可以作 .在 上任意取两点 , ,连同圆心 得到三个点,过其中的任意两点可以作直线与 相交.
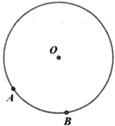 (1)、基于已知的三个点用直尺作出尽可能多的不同长度的线段,写出作法,并指出作出的线段;(2)、若 ,用含有 , 的式子写出能作出的所有线段的长度,请简要写出计算过程;(3)、能统一用一个公式写出能作出的所有线段的长度吗?22. 现代电视屏幕尺寸的设计,主要追求以下目标:一是更符合人体工程学要求(宽与长的比接近与0.618);二是设计适当的长宽比使屏幕的面积尽可能大现行的电视机屏幕有“宽屏”和“普屏”两种制式,宽屏的长宽比为 ;普屏的长宽比为 .
(1)、基于已知的三个点用直尺作出尽可能多的不同长度的线段,写出作法,并指出作出的线段;(2)、若 ,用含有 , 的式子写出能作出的所有线段的长度,请简要写出计算过程;(3)、能统一用一个公式写出能作出的所有线段的长度吗?22. 现代电视屏幕尺寸的设计,主要追求以下目标:一是更符合人体工程学要求(宽与长的比接近与0.618);二是设计适当的长宽比使屏幕的面积尽可能大现行的电视机屏幕有“宽屏”和“普屏”两种制式,宽屏的长宽比为 ;普屏的长宽比为 . (1)、哪种屏幕更适合人体工程学要求?请说明理由.(2)、一般地,电视屏幕的“几寸”指的是这个屏幕的长方形的对角线长有多少英寸,1英寸 ,小明家想买80寸的宽屏电视机(边框宽都为 ),并嵌入到墙中.则需要预留的长方形位置的长、宽各多少 ?(最后结果保留到整数, , )(3)、在相同尺寸的电视机屏幕中,宽屏的屏幕面积大还是普屏的屏幕面积大?请说明理由.23. 如图, 是 的直径, 是 上的一点,过点 作 的切线 ,过圆心 作 的平行线交直线 于点 ,交 于点 ,交 于点 ,连接 .
(1)、哪种屏幕更适合人体工程学要求?请说明理由.(2)、一般地,电视屏幕的“几寸”指的是这个屏幕的长方形的对角线长有多少英寸,1英寸 ,小明家想买80寸的宽屏电视机(边框宽都为 ),并嵌入到墙中.则需要预留的长方形位置的长、宽各多少 ?(最后结果保留到整数, , )(3)、在相同尺寸的电视机屏幕中,宽屏的屏幕面积大还是普屏的屏幕面积大?请说明理由.23. 如图, 是 的直径, 是 上的一点,过点 作 的切线 ,过圆心 作 的平行线交直线 于点 ,交 于点 ,交 于点 ,连接 . (1)、判断 与 的位置关系,并证明结论;(2)、若四边形 是平行四边形,求 的值;(3)、若 运动后能与 重合,则 , 请说明图形的运动过程.24. 某种鱼迁入一生态系统后.在无人为干预的条件下.这种鱼的种群在10个生长周期内的自然生长速率(数量增长的百分率)与时间的关系如下表(每周期约3个月):
(1)、判断 与 的位置关系,并证明结论;(2)、若四边形 是平行四边形,求 的值;(3)、若 运动后能与 重合,则 , 请说明图形的运动过程.24. 某种鱼迁入一生态系统后.在无人为干预的条件下.这种鱼的种群在10个生长周期内的自然生长速率(数量增长的百分率)与时间的关系如下表(每周期约3个月):第0周期|
第1周期
第2周期
第3周期
第4周期
生长速率(%)
0
18
32
42
48
这种鱼种群的数量增加到一定程度后,由于受生态制约,不再增加.
(1)、在无人为干预条件下,选择适当的函数模型描述该鱼种群的自然生长速率随生长周期变化的规律,写出函数解析式;(2)、在无人为干预条件下,用函数图象描述该鱼种群数量与生长周期之间的关系,则下列 , , 三个图象中最合理的是哪一个图象?请说明理由.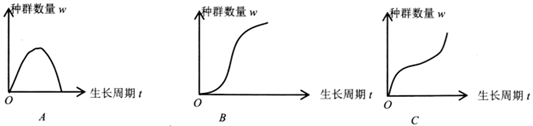 (3)、为了保证该鱼种群的可持续生长,考虑在适当时机进行捕获,问:最佳捕获时期是哪个时期?请说明理由.
(3)、为了保证该鱼种群的可持续生长,考虑在适当时机进行捕获,问:最佳捕获时期是哪个时期?请说明理由.