河南省漯河市舞阳县2021届九年级数学上学期数学期末考试卷
试卷更新日期:2021-01-13 类型:期末考试
一、单选题
-
1. 下列手机手势解锁图案中,是中心对称图形的是( )A、
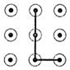 B、
B、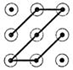 C、
C、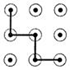 D、
D、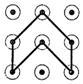 2. 已知 的半径是 ,圆心 到同一平面内直线 的距离为 ,则直线 与 的位置关系是( )A、相交 B、相切 C、相离 D、无法判断3. 已知反比例函数 ,下列结论中不正确的是( )A、图象必经过点 B、图象位于第二、四象限 C、若 ,则0< D、在每一个象限内, 随 值的增大而减小4. 在一幅长80cm,宽50cm的矩形风景画的四周镶上一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是5000cm2 , 设金色纸边的宽为xcm,那么满足的方程是( )
2. 已知 的半径是 ,圆心 到同一平面内直线 的距离为 ,则直线 与 的位置关系是( )A、相交 B、相切 C、相离 D、无法判断3. 已知反比例函数 ,下列结论中不正确的是( )A、图象必经过点 B、图象位于第二、四象限 C、若 ,则0< D、在每一个象限内, 随 值的增大而减小4. 在一幅长80cm,宽50cm的矩形风景画的四周镶上一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是5000cm2 , 设金色纸边的宽为xcm,那么满足的方程是( ) A、x2+130x﹣1400=0 B、x2﹣130x﹣1400=0 C、x2+65x﹣250=0 D、x2﹣65x﹣250=05. 在一个不透明的袋子中,装有红色、黑色、白色的玻璃球共有40个,除颜色外其它完全相同.若小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在 .和 ,则该袋子中的白色球可能有( )A、6个 B、16个 C、18个 D、24个6. 已知电流I(安培)、电压U(伏特)、电阻R(欧姆)之间的关系为 ,当电压为定值时,I关于R的函数图象是( )A、
A、x2+130x﹣1400=0 B、x2﹣130x﹣1400=0 C、x2+65x﹣250=0 D、x2﹣65x﹣250=05. 在一个不透明的袋子中,装有红色、黑色、白色的玻璃球共有40个,除颜色外其它完全相同.若小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在 .和 ,则该袋子中的白色球可能有( )A、6个 B、16个 C、18个 D、24个6. 已知电流I(安培)、电压U(伏特)、电阻R(欧姆)之间的关系为 ,当电压为定值时,I关于R的函数图象是( )A、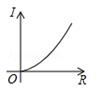 B、
B、 C、
C、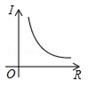 D、
D、 7. 如图, 是 的直径, 切 于点 , 交 于点 ;连接 ,若 ,则 等于( )
7. 如图, 是 的直径, 切 于点 , 交 于点 ;连接 ,若 ,则 等于( )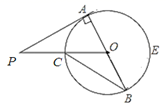 A、20° B、25° C、30° D、40°8. 如图,AB为⊙O的直径,点C在⊙O上,若 , ,则 的长为( )
A、20° B、25° C、30° D、40°8. 如图,AB为⊙O的直径,点C在⊙O上,若 , ,则 的长为( )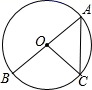 A、 B、 C、 D、9. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则以下结论同时成立的是
A、 B、 C、 D、9. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则以下结论同时成立的是 A、 B、 C、 D、10. 如图, 中, ,正方形 的顶点 别在 边上,设 的长度为 , 与正方形 重叠部分的面积为 ,则下列图象中能表示 与 之间的函数关系的是( )
A、 B、 C、 D、10. 如图, 中, ,正方形 的顶点 别在 边上,设 的长度为 , 与正方形 重叠部分的面积为 ,则下列图象中能表示 与 之间的函数关系的是( ) A、
A、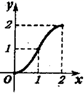 B、
B、 C、
C、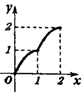 D、
D、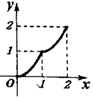
二、填空题
-
11. 已知: 是反比例函数,则m= .12. 如图△ABC中,∠A=30°,∠C=90°,作△ABC的外接圆.若弧AB的长为12cm,那么弧AC的长是.
 13. 一圆锥的母线长为6cm,它的侧面展开图的圆心角为120°,则这个圆锥的底面半径r=cm.14. 已知 的直径 , 是 的弦, ,垂足为 ,且 ,则 的长为cm.15. 从3,0,-1,-2,-3这五个数中.随机抽取一个数,作为函数 和关于x的方程 中m的值,恰好使函数的图象经过第一、三象限,且方程有实数根的概率是
13. 一圆锥的母线长为6cm,它的侧面展开图的圆心角为120°,则这个圆锥的底面半径r=cm.14. 已知 的直径 , 是 的弦, ,垂足为 ,且 ,则 的长为cm.15. 从3,0,-1,-2,-3这五个数中.随机抽取一个数,作为函数 和关于x的方程 中m的值,恰好使函数的图象经过第一、三象限,且方程有实数根的概率是.
三、解答题
-
16. 解方程:(1)、(2)、 .17. 现有一张演唱会的门票,小明与小华为了决定谁拿这张门票去看开幕式,小华设计了一种方案如下:如图,有 、 两个转盘,其中转盘 被分成3等份,转盘 被分成4等份,并在每一份内标上数字.两人同时分别转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将 转盘指针指向的数字记为 , 转盘指针指向的数字记为 ,从而确定点 的坐标为 .
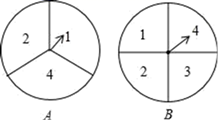 (1)、请用列表或画树状图的方法写出所有可能得到的点 的坐标;(2)、小华提议,在(1)的基础上,若点 落在反比例函数 图象上则小明赢;否则,自己赢.你觉得小华的提议对双方公平吗?请说明理由.18. 在下列网格图中,每个小正方形的边长均为1个单位长度.在 中, , , .
(1)、请用列表或画树状图的方法写出所有可能得到的点 的坐标;(2)、小华提议,在(1)的基础上,若点 落在反比例函数 图象上则小明赢;否则,自己赢.你觉得小华的提议对双方公平吗?请说明理由.18. 在下列网格图中,每个小正方形的边长均为1个单位长度.在 中, , , .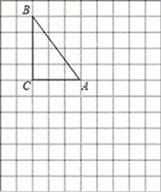
( 1 )试在图中做出 以 为旋转中心,沿顺时针方向旋转90°后的图形 ;
( 2 )若点 的坐标为 ,试在图中画出直角坐标系,并标出 , 两点的坐标;
( 3 )根据(2)的坐标系作出与 关于原点对称的图形 ,并标出 , 两点的坐标.
19. 如图,一次函数y1=﹣2x+b与反比例函数为y2= 的图象交于点A(﹣1,6),B(a,﹣2)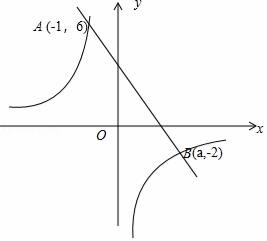 (1)、求反比例函数y2= 的解析式并求出a的值;(2)、根据图象直接写出y1>y2时,x的取值范围.20. 如图, 是 的直径, 切 于点 ,点 是 上的一点,且 , .
(1)、求反比例函数y2= 的解析式并求出a的值;(2)、根据图象直接写出y1>y2时,x的取值范围.20. 如图, 是 的直径, 切 于点 ,点 是 上的一点,且 , .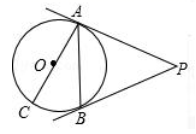 (1)、求证: 是 的切线;(2)、若 的半径为2,求弦 及 , 的长.21. 如图,点 为 斜边 上的一点,以 为半径的 与 切于点 ,连接 .
(1)、求证: 是 的切线;(2)、若 的半径为2,求弦 及 , 的长.21. 如图,点 为 斜边 上的一点,以 为半径的 与 切于点 ,连接 .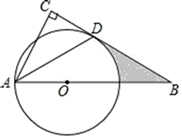 (1)、求证: 平分 ;(2)、若 , ,求阴影部分的面积(结果保留 )22. 如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数(k>0)的图象与BC边交于点E.
(1)、求证: 平分 ;(2)、若 , ,求阴影部分的面积(结果保留 )22. 如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数(k>0)的图象与BC边交于点E. (1)、当F为AB的中点时,求该函数的解析式;(2)、当k为何值时,△EFA的面积最大,最大面积是多少?23. 如图,已知抛物线 的图象的顶点坐标是 ,并且经过点 ,直线 与抛物线交于 , 两点,以 为直径作圆,圆心为点 ,圆 与直线 交于对称轴右侧的点 ,直线 上每一点的纵坐标都等于1.
(1)、当F为AB的中点时,求该函数的解析式;(2)、当k为何值时,△EFA的面积最大,最大面积是多少?23. 如图,已知抛物线 的图象的顶点坐标是 ,并且经过点 ,直线 与抛物线交于 , 两点,以 为直径作圆,圆心为点 ,圆 与直线 交于对称轴右侧的点 ,直线 上每一点的纵坐标都等于1.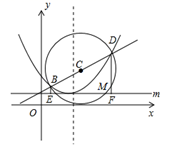 (1)、求抛物线的解析式;(2)、证明:圆 与 轴相切;(3)、过点 作 ,垂足为 ,再过点 作 ,垂足为 ,求 的值.(或者求 的值)
(1)、求抛物线的解析式;(2)、证明:圆 与 轴相切;(3)、过点 作 ,垂足为 ,再过点 作 ,垂足为 ,求 的值.(或者求 的值)