浙教版备考2021年中考数学一轮复习专题5——一元一次方程及其应用

试卷更新日期：2021-01-13 类型：一轮复习

进入出卷网下载

一、单选题

1. 下列方程中，是一元一次方程的为（）

A、3x+2y=6 B、4x-2=x+1 C、x²+2x-1=0 D、 $\frac{3}{x}$ -3= $\frac{1}{2}$

查看试题解析
2. 解一元一次方程 $\frac{1}{2}$ （x+1）＝1﹣ $\frac{1}{3}$ x时，去分母正确的是（）

A、3（x+1）＝1﹣2x B、2（x+1）＝1﹣3x C、2（x+1）＝6﹣3x D、3（x+1）＝6﹣2x

查看试题解析
3. 若 $x + y = 2$ ， $z - y = - 3$ ，则 $x + z$ 的值等于（）

A、5 B、1 C、-1 D、-5

查看试题解析
4. 下列方程的解是 $x = 3$ 的有（）
① $- 2 x - 6 = 0$ ② $| x + 2 | = 5$ ③ $(x - 3) (x - 1) = 0$ ④ $\frac{1}{3} x = x - 2$

A、1个 B、2个 C、3 D、4个

查看试题解析
5. 已知 $x = 2$ 是方程 $5 a - x = 13$ 的解，则a的值为（）

A、4 B、3 C、2 D、1

查看试题解析
6. 在实数范围内定义运算“☆”： $a ☆ b = a + b - 1$ ，例如： $2 ☆ 3 = 2 + 3 - 1 = 4$ .如果 $2 ☆ x = 1$ ，则x的值是（）.

A、-1 B、1 C、0 D、2

查看试题解析
7. 某品牌衬衫进价为120元，标价为240元，商家规定可以打折销售，但其利润率不能低于 $20%$ ，则这种品牌衬衫最多可以打几折？（）

A、8 B、6 C、7 D、9

查看试题解析
8. 方程 |x-5|+|x-7|=|x-2015|+|x-2013| 的解有（）个．

A、0 B、1 C、2 D、多于2个

查看试题解析
9. 《孙子算经》中有一道题，原文是：今有三人共车，一车空：二人共车，九人步，问人与车各几何？译文为：今有若干人乘车，每3人共乘一车，最终剩余2辆车：若每2人共乘一车，最终剩余9个人无车可乘，问共有多少人，多少辆车？设共有x人，可列方程（）

A、 $\frac{x + 2}{3} = \frac{x}{2} - 9$ B、 $\frac{x}{3} + 2 = \frac{x - 9}{2}$ C、 $\frac{x}{3} - 2 = \frac{x + 9}{2}$ D、 $\frac{x - 2}{3} = \frac{x}{2} + 9$

查看试题解析
10. 某车间有26名工人，每人每天可以生产800个螺钉或1000个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套，设安排m名工人生产螺钉，则下面所列方程正确的是（）

A、2×1000（26-m）=800m B、1000×（13-m）=800m C、1000×（26-m）=2×800m D、1000×（26-m）=800m

查看试题解析
11. 一项工程，甲单独做需10天完成，乙单独完成需6天完成．现由甲先做2天，乙再加入合做，完成这项工程需多少天？若设完成这项工程共需x天，依题意可得方程（）

A、 $\frac{x}{10} + \frac{x}{6} = 1$ B、 $\frac{x + 2}{10} + \frac{x - 2}{6} = 1$ C、 $\frac{x}{10} + \frac{x - 2}{6} = 1$ D、 $\frac{2}{x} + \frac{x - 2}{10} + \frac{x - 2}{6} = 1$

查看试题解析

二、填空题

12. 若 $(m - 2) x^{m^{2} - 3} - 5 = 0$ 是关于x的一元一次方程，则m的值为．

查看试题解析
13. $5$ 与 $x$ 的差等于 $x$ 的 $2$ 倍，根据前面的描述直接列出的方程是．

查看试题解析
14. 一个书包的标价为115元，按8折出售仍可获利15%，该书包的进价为元。

查看试题解析
15. 当x=时，两个代数式1+x²，x²-2x+3的值相等。

查看试题解析
16. 篮球联赛中，每玚比赛都要分出胜负，每队胜1场得2分，负1场得1分.某队14场比赛得到23分，则该队胜了场.

查看试题解析
17. 我们知道无限循环小数都可以化成分数．例如：将 $0. \overset{\cdot}{6}$ 化成分数时，可设 $0. \overset{\cdot}{6}$ =x，则有 $6. \overset{\cdot}{6} = 10 x$ ， $10 x = 6 + 0. \overset{\cdot}{6}$ ， $10 x = 6 + x$ ，解得 $x = \frac{2}{3}$ ，即 $0. \overset{\cdot}{6}$ 化成分数是 $\frac{2}{3}$ ．仿此方法，将 $0. \overset{\cdot}{6} \overset{\cdot}{3}$ 化成分数是．

查看试题解析

18. 有三个房间需要粉刷，粉刷方案要求:每个房间只用一种颜色的涂料，且三个房间的颜色各不相同. 三个房间的粉刷面积和三种颜色的涂料费用如下表:

房间A	房间B	房间C		涂料1	涂料2	涂料3
35m²	20m²	28m²		16元/m²	18元/m²	20元/m²

那么在所有不同的粉刷方案中，最低的涂料总费用是元.

查看试题解析

19. 鸡兔同笼是我国古代著名趣题之一，书中是这样叙述的：“今有雉兔同笼，上有三十五头下有九十四足，问雉兔各几何?意思是有若干只鸡兔在同一个笼子里从上面数有35个头，从下面数有94只脚，则笼子中鸡只，兔只。

查看试题解析
20.
长为1，宽为a的矩形纸片（ $\frac{1}{2} < a < 1$ ），如图那样折一下，剪下一个边长等于矩形宽度的正方形（称为第一次操作）；再把剩下的矩形如图那样折一下，剪下一个边长等于此时矩形宽度的正方形（称为第二次操作）；如此反复操作下去．若在第n此操作后，剩下的矩形为正方形，则操作终止．当n=3时，a的值为．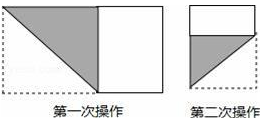

查看试题解析

三、综合题

21. 解方程：

(1)、2（3x﹣1）=16；

(2)、 $\frac{x + 1}{4} - 1 = \frac{2 x + 1}{6}$ ；

(3)、 $\frac{x}{0.3} - \frac{1.5 - 2 x}{0.2} = 1$

查看试题解析
22. 以下是圆圆解方程 $\frac{x + 1}{2} - \frac{x - 3}{3} = 1$ 的解答过程。
解：去分母，得3(x+1)-2(x-3)=1。

去括号，得3x+1-2x+3=1。

移项，合并同类项，得x=-3。

圆圆的解答过程是否有错误？如果有错误，写出正确的解答过程。

查看试题解析
23. 如图，某课外活动小组利用一面墙（墙足够长），另三边用20m长的篱笆围成一个面积为50m²的矩形花园ABCD，求边AB、BC的长。

查看试题解析
24. 中国古代数学著作《孙子算经》中有这样一个问题，原文：今有三人共车，二车空；二人共车，九人步，人与车各几何？译文为：今有若干人乘车，每3人共乘一车，所乘车都坐满，最终剩余2辆车，若每2人共乘一车，最终剩余9个人无车可乘，问共有多少人，多少辆车？

查看试题解析
25. 用列代数式或列方程（组）的方法，解决网络上流行的一个问题：法国新总统比法国第一夫人小24岁，美国新总统比美国第一夫人大24岁，法国新总统比美国新总统小32岁．求：美国第一夫人比法国第一夫人小多少岁？

查看试题解析
26. 某企业生产的一种果汁饮料由A、B两种水果配制而成，其比例与成本如下方表格所示，已知该饮料的成本价为8元/千克，按现价售出后可获利润50%，每个月可出售27500瓶.

每千克饮料所占比例

成本（元/千克）

A

20%

m

B

80%

m-15

(1)、求m的值；

(2)、由于物价上涨，A水果成本提高了25%，B水果成本提高了20%，在不改变售价的情况下，若要保持每个月的利润不减少，则现在至少需要售出多少瓶饮料？

查看试题解析
27. 建材市场为某工厂代销一种建筑材料．当每吨售价为260元时，月销售量为45吨．该经销店为提高经营利润，准备采取降价的方式进行促销．经市场调查发现：当每吨售价每下降10元时，月销售量就会增加7.5吨．综合考虑各种因素，每售出一吨建筑材料共需支付厂家及其他费用100元．

(1)、当每吨售价是240元时，计算此时的月销售量；

(2)、为进一步推广品牌，尽可能的扩大销量，当每吨材料售价为多少时，该经销店月利润为9000元？

(3)、有人说“当月利润最大时，月销售额也最大．”你认为对吗？请说明理由．

查看试题解析

28. 甲，乙两人沿湖边环形道上匀速跑步，他们开启了微信运动﹣﹣微信上实时统计每天步数的软件.已知乙的步距比甲的步距少0.4m(步距是指每一步的距离)，且每2分钟甲比乙多跑25步，两人各跑3周后到达同一地点，跑3圈前后的时刻和步数如下：

	出发时刻	出发时微信运动中显示的步数	结束时刻	结束时微信运动中显示的步数
甲	9：30	2158	9：40	4158
乙	a	1308	9：40	4308

(1)、求甲，乙的步距和环形道的周长；

(2)、求表中a的值；

(3)、若两人于9：40开始反向跑，问：此后，当微运动中显示的步数相差50步时，他们相遇了几次？

查看试题解析

29. 自2016年1月1日起，某市居民生活用水实施年度阶梯水价，具体水价标准见下表：

类别	水费价格（元/立方米）	污水处理费（元/立方米）	综合水价（元/立方米）
第一阶梯≤120（含）立方米	3.5	1.5	5
第二阶梯120～180（含）立方米	5.25	1.5	6.75
第三阶梯＞180立方米	10.5	1.5	12

例如，某户家庭年用水124立方米，应缴纳水费：120x5+（124﹣120）x6.75＝627（元）.

(1)、小华家2017年共用水150立方米，则应缴纳水费多少元？

(2)、小红家2017年共用水m立方米（m＞200），请用含m的代数式表示应缴纳的水费.

(3)、小刚家2017年，2018年两年共用水360立方米，已知2018年的年用水量少于2017年的年用水量，两年共缴纳水费2115元，求小刚家这两年的年用水量分别是多少？

查看试题解析

	每千克饮料所占比例	成本（元/千克）
A	20%	m
B	80%	m-15