浙江省绍兴市2021届九年级上学期数学12月月考试卷

试卷更新日期：2021-01-12 类型：月考试卷

进入出卷网下载

一、选择题（本题共10小题，每小题4分，共40分）

1. 若 $\frac{a}{b} = \frac{3}{4}$ ，则 $\frac{a + b}{b}$ =（）

A、2 B、 $\frac{7}{4}$ C、 $\frac{5}{4}$ D、 $\frac{3}{2}$

查看试题解析
2. 将抛物线y=﹣x²向左平移2个单位后，得到的抛物线的解析式是（）

A、y=﹣（x+2）² B、y=﹣x²+2 C、y=﹣（x﹣2）² D、y=﹣x²﹣2

查看试题解析
3. 下列说法中错误的是（）

A、某种彩票的中奖率为1％，买100张彩票一定有1张中奖 B、从装有10个红球的袋子中，摸出1个白球是不可能事件 C、为了解一批日光灯的使用寿命，可采用抽样调查的方式 D、掷一枚普通的正六面体骰子，出现向上一面点数是2的概率是 $\frac{1}{6}$

查看试题解析
4. 已知（﹣1，y₁），（﹣2，y₂），（﹣4，y₃）是抛物线y=﹣2x²﹣8x+m上的点，则（　　）

A、y₁＜y₂＜y₃ B、y₃＜y₂＜y₁ C、y₃＜y₁＜y₂ D、y₂＜y₃＜y₁

查看试题解析
5. 如图，AB，CD都垂直于x轴，垂足分别为B，D，若A（6，3），C（2，1），
则△OCD与四边形ABDC的面积比为（）

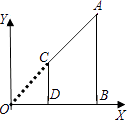A、1：2 B、1：3 C、1：4 D、1：8

查看试题解析
6. 如图，二次函数y=ax²+bx+c的图象开口向上，对称轴为直线x=1，图象经过（3，0）．下列结论中，正确的一项是（）

A、 $a b c$ ＜0 B、 $2 a + b$ ＜0 C、 $a - b + c$ ＜0 D、4ac−b² $<$ 0

查看试题解析
7. 如图所示，在平行四边形ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则DF：FC=（）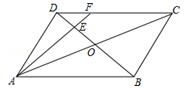

A、1：4 B、1：3 C、2：3 D、1：2

查看试题解析
8. 如图，A，B，C三点在圆上，在△ABC中，∠ABC=70°，∠ACB=30°，D是弧BAC的中点，连结DB，DC，则∠DBC的度数为（　　）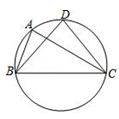

A、70° B、50° C、45° D、30°

查看试题解析
9. 下列语句中，正确的是（）
①三个点确定一个圆；②同弧或等弧所对的圆周角相等；③平分弦的直径垂直于弦，并且平分弦所对的弧；④圆内接平行四边形一定是矩形．

A、①② B、②③ C、②④ D、④

查看试题解析
10. 在 $△ A B C$ 中，点 $D$ 在 $A B$ 上，点 $E$ 在 $A C$ 上，且 $△ A D E$ 与 $△ A B C$ 相似， $A D = E C$ ， $B D = 10$ ， $A E = 4$ ，则 $A B$ 的长为（）

A、 $2 \sqrt{10}$ B、12 C、 $2 \sqrt{10} + 10$ D、 $12$ 或 $2 \sqrt{10} + 10$

查看试题解析

二、填空题（本题共6小题，每小题5分，共30分）

11. 已知线段a=3，b=27，则a，b的比例中项线段长等于.

查看试题解析
12. 如图，已知点C是弧AB上的一点，圆周角∠ACB为125°，则圆心角∠AOB=度.

查看试题解析
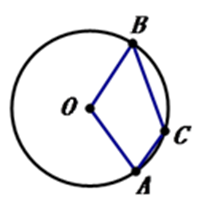13. 二次函数y=ax²﹣3ax+2（a＜0）的图象如图所示，若y＜2，则x的取值范围为.

查看试题解析
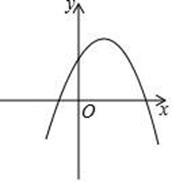14. 如图，P是△ABC的重心，过点P作PE∥AB交BC于点E，PF∥AC交BC于点F，若△PEF的周长是6，则△ABC的周长为.

查看试题解析
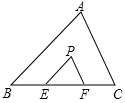15. 如图，点O是半径为3的圆形纸片的圆心，将这个圆形纸片按下列顺序折叠，使 $\overset{⌢}{A B}$ 和 $\overset{⌢}{A C}$ 都经过圆心O，则阴影部分面积是。

查看试题解析
16. 如图，平行于x轴的直线AC分别交抛物线 y= x²（x≥0）与 $y = \frac{x^{2}}{5}$ （x≥0）于点B、C，过点C作y轴的平行线交y= x²于点D，直线DE∥AC，交 $y = \frac{x^{2}}{5}$ 于点E，则 $\frac{D E}{A B}$ =.

查看试题解析

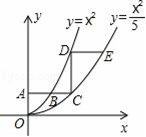
三、解答题（本题共8 小题，共80分）

17. 如图，D是△ABC的边AC上的一点，连接BD，已知∠ABD=∠C.

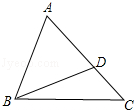(1)、求证：△ABD∽△ACB

(2)、若AB=6，AD=4，求线段CD的长

查看试题解析
18. 如图所示，AB是⊙O的一条弦，OD⊥AB，垂直为C，交⊙O于点D，点E在⊙O上；

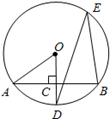(1)、若∠AOD=52°，求∠DEB的度数；

(2)、若OC=3，OA=5，求AB的长.

查看试题解析
19. 如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=(x-1)²-4，AB为半圆的直径，求这个“果圆”被y轴截得的弦CD的长.

查看试题解析
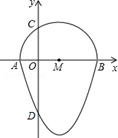20.
某商场设定了一个可以自由转动的转盘（转盘被等分成16个扇形），并规定：顾客在商场消费每满200元，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红、黄和蓝色区域，顾客就可以分别获得50元、30元和10元的购物券．如果顾客不愿意转转盘，则可以直接获得购物券15元．

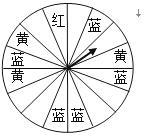(1)、转动一次转盘，获得50元、30元、10元购物券的概率分别是多少？

(2)、如果有一名顾客在商场消费了200元，通过计算说明转转盘和直接获得购物券，哪种方式对这位顾客更合算？

查看试题解析
21. 某农场拟建三间矩形饲养室，饲养室一面靠墙（墙可用长≤20m），中间用两道墙隔开，已知计划中的建筑材料可建围墙的总长为60m，设饲养室宽为x（m），总占地面积为y（m²）（如图所示）.

(1)、求y关于x的函数表达式，并直接写出自变量x的取值范围；

(2)、三间饲养室占地总面积有可能达到210m²吗？请说明理由.

查看试题解析
22. 如图，在Rt△ABC中，∠BAC=90°，AB=6，AC=8，点D为边BC的中点，点P为射线AB上的一动点，点Q为边AC上的一动点，且∠PDQ=90°.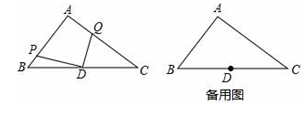

(1)、当DP⊥AB时，求CQ的长；

(2)、当BP=2，求CQ的长

查看试题解析
23. 函数 $y = - \frac{3}{4} x - 12$ 的函数图象分别交x轴、y轴于A，C两点.

(1)、求A，C两点的坐标.

(2)、在x轴上找出点B，使△ACB∽△AOC，求B的坐标，若抛物线经过A.B.C三点，求出抛物线的函数解析式.

(3)、若在（2）的条件下，设动点P、Q分别从A、B两点同时出发，以相同的速度沿AC、BA向C、A运动，连结PQ，设AP=m.问是否存在m，使以A、P、Q为顶点的三角形与△ABC相似?若存在，求出所有m的值；若不存在说明理由

查看试题解析
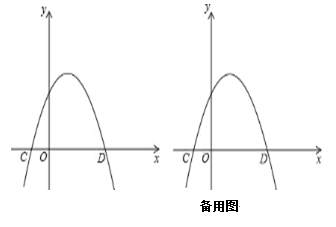24. 在平面直角坐标系 $x o y$ 中，规定：抛物线 $y = a {(x - h)}^{2} + k$ 的伴随直线为 $y = a (x - h) + k$ .例如：抛物线 $y = 2 {(x + 1)}^{2} - 3$ 的伴随直线为 $y = 2 (x + 1) - 3$ ，即 $y = 2 x - 1$

(1)、在上面规定下，抛物线 $y = {(x + 1)}^{2} - 4$ 的顶点为.伴随直线为；

(2)、若顶点在第一象限的抛物线 $y = m {(x - 1)}^{2} - 4 m$ 与其伴随直线相交于点A，B (点A在点B的左侧)，抛物线与x轴交于点C、D(点C在点D的左侧).
①若 $∠ C A B = 90 °$ 求m的值；
②如果点 $P (x ， y)$ 是直线BC上方抛物线的一个动点， $△ P B C$ 的面积记为S，当S取得最大值 $\frac{27}{4}$ 时，求m的值.

查看试题解析