浙江省衢州市2021届九年级上学期数学12月联考试卷

试卷更新日期：2021-01-12 类型：月考试卷

进入出卷网下载

一、选择题（本大题共有10小题，每小题3分，共30分.请选出每小题中最符合题意的一个选项，不选、多选、错选均不给分）

1. 若 $\frac{a}{3} = \frac{b}{7}$ ，则 $\frac{b - a}{a}$ 等于（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{7}{3}$ D、 $\frac{3}{7}$

查看试题解析
2. 已知抛物线 $y = - {(x + 3)}^{2} - 5$ ，则此抛物线的函数值有（）

A、最小值-3 B、最大值是-3 C、最小值是-5 D、最大值是-5

查看试题解析
3. 已知△ABC 与△A₁B₁C₁ 相似，且相似比为 1：3，则△ABC 与△A₁B₁C₁ 的面积比为（）

A、1：9 B、1：3 C、1：6 D、1：1

查看试题解析
4. 如图，AB是⊙O的直径，C，D是⊙O上的两点，若∠ABC=70°，则∠BDC的度数为（）

A、50° B、40° C、30° D、20°

查看试题解析
5. 下列说法正确的是（）

A、任意抛掷一枚质地均匀的硬币10次，则“有5次正面朝上”是必然事件 B、明天的降水概率为40%，则“明天下雨”是确定事件 C、篮球队员在罚球线上投篮一次，则“投中”是随机事件 D、a是实数，则“|a|≥0”是不可能事件

查看试题解析
6. 如图，已知⊙O为四边形ABCD的外接圆，O为圆心，若∠BCD=120°，AB=AD=2，则⊙O的半径长为（）

A、 $\frac{3}{2}$ B、 $\frac{\sqrt{6}}{2}$ C、 $\frac{3 \sqrt{2}}{2}$ D、 $\frac{2 \sqrt{3}}{3}$

查看试题解析
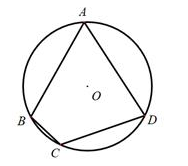7. 把抛物线y＝2x²－1先向右平移2个单位，再向下平移1个单位，所得抛物线的解析式为（）

A、y＝2x²＋8x＋6 B、y＝2x²－8x＋6 C、y＝2x²－8x＋8 D、y＝2x²－8x－8

查看试题解析
8. 如图，为了测量旗杆AB的高度，小凡在距旗杆底部B点10.8米的C点处放置了一面镜子，然后沿着直线BC后退到点E，恰好能从镜子中观察到旗杆顶部的A点.已知小凡眼睛所在的D点离地面的高度是1.6米，CE=2.7米，则旗杆AB的高度是（　　）

A、6.4米 B、7.2米 C、8米 D、9.6米

查看试题解析
9. 如图，在 $⊙ O$ 中， $O A = 2$ ， $∠ C = 45 °$ ，则图中阴影部分的面积为（）

A、 $\frac{π}{2} - \sqrt{2}$ B、 $π - \sqrt{2}$ C、 $\frac{π}{2} - 2$ D、 $π - 2$

查看试题解析
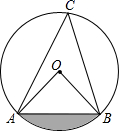10. 如图，在△ABC中，∠C=90°，AB=10cm，BC=8cm，点P从点A沿AC向点C以1cm/s的速度运动，同时点Q从点C沿CB向点B以2cm/s的速度运动（点Q运动到点B停止），在运动过程中，四边形PABQ的面积最小值为（）

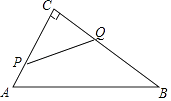A、19cm² B、16cm² C、15cm² D、12cm²

查看试题解析

二、填空题（本大题共6个小题,每小题4分，共24分，请将答案填在答题纸的对应位置上）

11. 抛物线 y=-(x+1)2+3的顶点坐标为.

查看试题解析
12. 一个不透明的袋子中装有 3 个小球，它们除分别标有的数字 1，3，5 不同外，其他完全相同.任意从袋子中摸出一球后放回，摇匀后再任意摸出一球，则两次摸出的球所标数字之和为 6 的概率是 .

查看试题解析
13. 如图，⊙O的半径OA等于5，半径OC与弦AB垂直，垂足为D，若OD＝3，则弦AB的长为.

查看试题解析
14. 如图，在平行四边形ABCD中，E是CD延长线上的一点，BE与AD相交于点F，CD=2DE.若△DEF的面积为2，则四边形DFBC的面积为.

查看试题解析
15. 如果矩形一边的两个端点与它对边上的一点所构成的角是直角，那么我们就把这个点叫做矩形的“直角点”，如图，如果E是矩形ABCD的一个“直角点”，且CD=3EC，那么AD：AB的值是.

查看试题解析
16. 如图，正△ABO的边长为2，O为坐标原点，A在x轴上，B在第二象限，△ABO沿x轴正方形作无滑动的翻滚，经一次翻滚后得到△A₁B₁O，则翻滚3次后点B的对应点的坐标是，翻滚2020次后AB中点M经过的路径长为.

查看试题解析

三、解答题（本大题共8小题，共66分.解答应写出必要的文字说明、证明过程或演算步骤）

17. 计算： $\sqrt{9} - | - 2 | + {(\sqrt{3} - 1)}^{0} - (- 2)$

查看试题解析
18. 已知△ABC在平面直角坐标系内，三个顶点的坐标分别为A（0，3），B（4，5），C（3，2）（正方形网格中，每个小正方形的边长都是1个单位长度）.

（ 1 ）画出△ABC向下平移5个单位长度得到的△A₁B₁C₁ ，并直接写出点C₁的坐标；

（ 2 ）绕点O顺时针旋转90°得到△A₂B₂C₂ ，并求出扇形C₁OC₂的面积.

查看试题解析

19. 为了庆祝2020年元旦文艺汇演，某县决定开展“唱响新时代，演绎青春光彩”主题演讲比赛，某中学将参加本校选拔赛的40名选手的成绩(满分为100分，得分为正整数且无满分，最低为75分)分成五组，并绘制了下列不完整的统计图表.

分数段	频数	频率
74.5∼79.5	2	0.05
79.5∼84.5	m	0.2
84.5∼89.5	12	0.3
89.5∼94.5	14	n
94.5∼99.5	4	0.1

(1)、表中m = ， n =；

(2)、请在图中补全频数直方图；

(3)、选拔赛中，成绩在94.5分以上的选手，男生和女生各占一半，学校从中随机确定2名选手参加全县决赛，请用列举法或树状图法求恰好是一名男生和一名女生的概率.

查看试题解析

20. 周末，小华和小亮想用所学的数学知识测量家门前小河的宽.测量时，他们选择了河对岸岸边的一棵大树，将其底部作为点A，在他们所在的岸边选择了点B，使得AB与河岸垂直，并在B点竖起标杆BC，再在AB的延长线上选择点D，竖起标杆DE，使得点E与点C. A共线.

已知：CB⊥AD，ED⊥AD，测得BC=1m，DE=1.5m，BD=8.5m.测量示意图如图所示.请根据相关测量信息，求河宽AB.

查看试题解析
21. 如图，在△ABC中，AB=AC，⊙O是△ABC的外接圆，D为弧AC的中点，E是BA延长线上一点，∠DAE=105°.

(1)、求∠CAD的度数；

(2)、若⊙O的半径为4，求弧BC的长.

查看试题解析
22. 网络销售是一种重要的销售方式.某乡镇农贸公司新开设了一家网店，销售当地农产品.其中一种当地特产在网上试销售，其成本为每千克2元.公司在试销售期间，调查发现，每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中2<x⩽10).

(1)、若5<x⩽10，求y与x之间的函数关系式；

(2)、销售单价x为多少元时，每天的销售利润最大?最大利润是多少元?

查看试题解析
23. 已知：如图，在菱形ABCD中，点E、F分别在边AB、AD上，BE＝DF，CE的延长线交DA的延长线于点G，CF的延长线交BA的延长线于点H.

(1)、求证：△BEC∽△BCH；

(2)、如果BE²＝AB•AE，求证：AG＝DF.

查看试题解析
24. 如图已知直线y= $\frac{1}{2}$ x+ $\frac{1}{2}$ 与抛物线y=ax²+bx+c相交于A(−1，0)，B(4，m)两点，抛物线y=ax²+bx+c交y轴于点C(0， $- \frac{3}{2}$ )，交x轴正半轴于D点，抛物线的顶点为M.

(1)、求抛物线的解析式；

(2)、设点P为直线AB下方的抛物线上一动点，当△PAB的面积最大时，求△PAB的面积及点P的坐标；

(3)、若点Q为x轴上一动点，点N在抛物线上且位于其对称轴右侧，当△QMN与△MAD相似时，直接写出N点的坐标.

查看试题解析