浙江省温州市乐清市2021届九年级上学期数学期中考试试卷

试卷更新日期：2021-01-12 类型：期中考试

进入出卷网下载

一、选择题（每题4分，共40分）

1. 抛物线y=﹣ $\frac{3}{5}$ （x+ $\frac{1}{2}$ ）²﹣3的顶点坐标是（）

A、（ $\frac{1}{2}$ ，﹣3） B、（﹣ $\frac{1}{2}$ ，﹣3） C、（ $\frac{1}{2}$ ，3） D、（﹣ $\frac{1}{2}$ ，3）

查看试题解析
2. 下列说法中，正确的是（）．

A、买一张电影票，座位号一定是奇数 B、投掷一枚均匀的硬币，正面一定朝上 C、从 $1$ ， $2$ ， $3$ ， $4$ ， $5$ 这五个数字中任意取一个数，取得奇数的可能性大 D、三个点一定可以确定一个圆

查看试题解析
3. “已知二次函数y＝ax²+bx+c的图象如图所示，试判断a+b+c与0的大小.”一同学是这样回答的：“由图象可知：当x＝1时y＜0，所以a+b+c＜0.”他这种说明问题的方式体现的数学思想方法叫做（）

A、换元法 B、配方法 C、数形结合法 D、分类讨论法

查看试题解析
4. 如图.点A，B，C，D，E均在⊙O上.∠BAC＝15°，∠CED＝30°，则∠BOD的度数为（）

A、45° B、60° C、75° D、90°

查看试题解析
5. 以下命题：
①三角形的内心是三角形三边中垂线的垂点；②任意三角形都有且只有一个外接圆；③圆周角相等，则弧相等.④经过两点有且只有一个圆，其中真命题的个数为（）个.

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，在△ABC中，点D、E分别在AB、AC上，DE∥BC，若AD＝2，DB＝1，△ADE、△ABC的面积分别为S₁、S₂ ，则 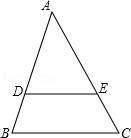$\frac{S_{1}}{S_{2}}$ 的值为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{4}{9}$ D、2

查看试题解析
7. 已知弦AB把圆周分成1：3的两部分，则弦AB所对的圆周角的度数为（）

A、45° B、90° C、90° 或27° D、45°或135°

查看试题解析
8. 如图，D是等腰△ABC外接圆弧AC上的点，AB＝AC且∠CAB＝56°，则∠ADC的度数为（）

A、116° B、118° C、122° D、126°

查看试题解析
9. 二次函数y=ax²﹣2ax+c的图象经过点（﹣1，0），则方程ax²﹣2ax+c=0解为（）

A、x₁=﹣3 x₂=﹣1 B、x₁=1 x₂=3 C、x₁=﹣1 x₂=3 D、x₁=﹣3 x₂=1

查看试题解析
10. 如图，四边形ABCD为⊙O的内接四边形.弦AB与DC的延长线相交于点G，AO⊥CD，垂足为E，连接BD，∠GBC＝48°，则∠DBC的度数为（）

A、84° B、72° C、66° D、48°

查看试题解析

二、填空题（每题3分，共18分）

11. △ABC为⊙O的内接三角形，若∠AOC＝160°，则∠ABC的度数是.

查看试题解析
12. 两个相似三角形的最短边分别是5cm和3cm，它们的周长之差是12cm，那么小三角形的周长为．

查看试题解析
13. 如图，在△ABC中，∠ACB＝90°，∠A＝30°，AB＝4，以点B为圆心，BC长为半径画弧，交边AB于点D，则CD的长为.

查看试题解析
14. 如图是一个游戏转盘，自由转动转盘，当转盘停止转动后，指针落在数字“Ⅱ”所示区域内的概率是.

查看试题解析
15. 如图，已知Rt△ABC中，∠C＝90°，BC＝8，AC＝6，CD是斜边AB上的高，求AD的长度为.

查看试题解析
16. 如图，抛物线y＝ax²+c（a＜0）交x轴于点G，F，交y轴于点D，在x轴上方的抛物线上有两点B，E，它们关于y轴对称，点G，B在y轴左侧，BA⊥OG于点A，BC⊥OD于点C，四边形OABC与四边形ODEF的面积分别为6和10，则△ABG与△BCD的面积之和为.

查看试题解析

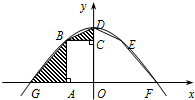
三、解答题（17-20每题6分，21-22题每题8分，23题10分，24题12分）

17. 已知：如图，在⊙O中，AB＝CD，AB与CD相交于点M.
求证：AM＝DM.

查看试题解析
18. 如图，一艘舰艇在海面下600米A处测得俯角为30°前下方的海底C处有黑匣子信号发出，继续在同一深度直线航行2000米后再次在B点处测得俯角为60°前下方的海底C处有黑匣子信号发出，求海底黑匣子C处距离海面的深度（结果保留根号）

查看试题解析
19. 一个布袋里装有4个只有颜色不同的球，其中3个红球，一个白球.从布袋里摸出一个球，记下颜色后放回，搅匀，再摸出1个球.求下列事件发生的概率：

(1)、事件A：摸出一个红球，1个白球.

(2)、事件B：摸出两个红球.

查看试题解析
20. 已知二次函数的图象经过点（0，3），顶点坐标为（1，4），

(1)、求这个二次函数的解析式；

(2)、求图象与x轴交点A、B两点的坐标；

(3)、图象与y轴交点为点C，求三角形ABC的面积.

查看试题解析
21. 如图，已知在⊙O中，两条弦AB和CD交于点P，且AP＝CP，求证：AB＝CD.

查看试题解析
22. 如图，已知AB是⊙O的直径，C、D是⊙O上的点，OC∥BD，交AD于点E，连结BC.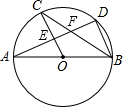

(1)、求证：AE＝ED；

(2)、若AB＝10，∠CBD＝36°，求弧AC的长及扇形AOC的面积.

查看试题解析
23. 夏季空调销售供不应求，某空调厂接到一份紧急订单，要求在10天内（含10天）完成任务，为提高生产效率，工厂加班加点，接到任务的第一天就生产了空调42台，以后每天生产的空调都比前一天多2台，由于机器损耗等原因，当日生产的空调数量达到50台后，每多生产一台，当天生产的所有空调，平均每台成本就增加20元．

(1)、设第x天生产空调y台，直接写出y与x之间的函数解析式，并写出自变量x的取值范围．

(2)、若每台空调的成本价（日生产量不超过50台时）为2000元，订购价格为每台2920元，设第x天的利润为W元，试求W与x之间的函数解析式，并求工厂哪一天获得的利润最大，最大利润是多少．

查看试题解析
24. 如图，在平面直角坐标系中，点A，B分别是y轴正半轴，x轴正半轴上两动点，OA＝2k，OB＝2k+3，以AO，BO为邻边构造矩形AOBC，抛物线y＝﹣ $\frac{3}{4} x^{2}$ +3x+k交y轴于点D，P为顶点，PM⊥x轴于点M.

(1)、求OD，PM的长（结果均用含k的代数式表示）.

(2)、当PM＝BM时，求该抛物线的表达式.

(3)、在点A在整个运动过程中，若存在△ADP是等腰三角形，请求出所有满足条件的k的值.

查看试题解析