宁夏银川市兴庆区2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2021-01-12 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、2x+3y=5xy B、4x-2x=2x2 C、-a2+a2=0 D、8a2b-5a2b=3a22. 如图,检测4个足球的质量,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从符合标准质量的角度看,最接近标准的是( )A、
 B、
B、 C、
C、 D、
D、 3. 电视剧《铁血将军》在我市拍摄,该剧展示了抗日英雄范筑先的光辉形象.某校为了解学生对“民族英雄范筑先”的知晓情况,从全校2400名学生中随机抽取了100名学生进行调查.在这次调查中,样本是( )A、2400名学生 B、100名学生 C、所抽取的100名学生对“民族英雄范筑先”的知晓情况 D、每一名学生对“民族英雄范筑先”的知晓情况4. 下列图形中,不是正方体的展开图的是( )
3. 电视剧《铁血将军》在我市拍摄,该剧展示了抗日英雄范筑先的光辉形象.某校为了解学生对“民族英雄范筑先”的知晓情况,从全校2400名学生中随机抽取了100名学生进行调查.在这次调查中,样本是( )A、2400名学生 B、100名学生 C、所抽取的100名学生对“民族英雄范筑先”的知晓情况 D、每一名学生对“民族英雄范筑先”的知晓情况4. 下列图形中,不是正方体的展开图的是( )
A、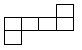 B、
B、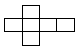 C、
C、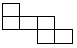 D、
D、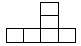 5.
5.如图是甲、乙两位同学某学期的四次数学考试成绩的折线统计图,则关于这四次数学考试成绩的说法正确的是( )
 A、甲成绩比乙成绩稳定 B、乙成绩比甲成绩稳定 C、甲、乙两成绩一样稳定 D、不能比较两人成绩的稳定性6. 王强同学在画数轴时只标了单位长度(一格表示单位长度为 )和正方向,而忘了标上原点(如图).若点 和点 表示的两个数的绝对值相等,则点 表示的数是( )
A、甲成绩比乙成绩稳定 B、乙成绩比甲成绩稳定 C、甲、乙两成绩一样稳定 D、不能比较两人成绩的稳定性6. 王强同学在画数轴时只标了单位长度(一格表示单位长度为 )和正方向,而忘了标上原点(如图).若点 和点 表示的两个数的绝对值相等,则点 表示的数是( ) A、-3 B、-2 C、2 D、37. 某次考试中,某班级的数学成绩统计图如图.下列说法错误的是( )
A、-3 B、-2 C、2 D、37. 某次考试中,某班级的数学成绩统计图如图.下列说法错误的是( )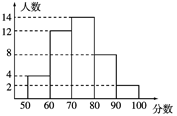 A、得分在70~80分之间的人数最多 B、该班的总人数为40 C、得分在90~100分之间的人数最少 D、及格(≥60分)人数是268. 线段 , 是 的中点, 是 的中点, 是 的中点, 是 的中点,依此类推,线段AC5的长为( )A、 B、 C、 D、
A、得分在70~80分之间的人数最多 B、该班的总人数为40 C、得分在90~100分之间的人数最少 D、及格(≥60分)人数是268. 线段 , 是 的中点, 是 的中点, 是 的中点, 是 的中点,依此类推,线段AC5的长为( )A、 B、 C、 D、二、填空题
-
9. 的相反数是.10. 温度由 下降 后是 .11. 中国的陆地面积约为9 600 000km2 , 把9 600 000用科学记数法表示为 .12. 下列几何体的截面是.
 13. 一个棱柱有8个面,则这个棱柱有条侧棱.14. 若 ,那么 的值是.15. 甲、乙两站相距 公里,一列慢车从甲站开往乙站,每小时行 公里,一列快车从乙站开往甲站,每小时行 公里.慢车从甲站开出 小时后,快车从乙站开出,那么快车开出小时后快车与慢车相距 公里.16. 用长为16m的铁丝沿墙围成一个长方形(墙的一面为该长方形的长,不用铁丝),该长方形的长比宽多1m,则该长方形的面积为m2.
13. 一个棱柱有8个面,则这个棱柱有条侧棱.14. 若 ,那么 的值是.15. 甲、乙两站相距 公里,一列慢车从甲站开往乙站,每小时行 公里,一列快车从乙站开往甲站,每小时行 公里.慢车从甲站开出 小时后,快车从乙站开出,那么快车开出小时后快车与慢车相距 公里.16. 用长为16m的铁丝沿墙围成一个长方形(墙的一面为该长方形的长,不用铁丝),该长方形的长比宽多1m,则该长方形的面积为m2.三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 解方程:19. 先化简,再求值 ,其中 x=3,y=-2.20. 一个几何体由几个大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面和从左面看到的这个几何体的形状图.
 21. 一种圆形的机器零件规定直径为200毫米,为检测它们的质量,从中抽取6件进行检测,比规定直径大的毫米数记作正数,比规定直径小的毫米数记作负数.检查记录如下:
21. 一种圆形的机器零件规定直径为200毫米,为检测它们的质量,从中抽取6件进行检测,比规定直径大的毫米数记作正数,比规定直径小的毫米数记作负数.检查记录如下:1
2
3
4
5
6
0.2
-0.1
-0.3
0.1
0
-0.2
(1)、第几号的机器零件直径最大?第几号最小?并求出最大直径和最小直径的长度;(2)、质量最好的是哪个?质量最差的呢?22. 某公园准备修建一块长方形草坪,长为30米,宽为20米.并在草坪上修建如图所示的十字路,已知十字路宽x米,回答下列问题: (1)、修建的十字路面积是多少平方米?(2)、如果十字路宽2米,那么草坪(阴影部分)的面积是多少?23. 张强到某城市行政中心大楼办事,假定乘电梯向上一楼记为+1,向下一楼记为-1.张强从1楼出发,电梯上下楼层依次记录如下(单位:层):+4,-3,+10,-8,+12,-6,-7.(1)、请你通过计算说明张强最后停在几楼;(2)、该中心大楼每层高2.8m,电梯每上或下1m需要耗电a度.根据张强现在所处的位置,请你算一算,当他办事时电梯需要耗电多少度?24. 为增强学生的身体素质,教育行政部门规定学生每天户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如图所示中两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)、修建的十字路面积是多少平方米?(2)、如果十字路宽2米,那么草坪(阴影部分)的面积是多少?23. 张强到某城市行政中心大楼办事,假定乘电梯向上一楼记为+1,向下一楼记为-1.张强从1楼出发,电梯上下楼层依次记录如下(单位:层):+4,-3,+10,-8,+12,-6,-7.(1)、请你通过计算说明张强最后停在几楼;(2)、该中心大楼每层高2.8m,电梯每上或下1m需要耗电a度.根据张强现在所处的位置,请你算一算,当他办事时电梯需要耗电多少度?24. 为增强学生的身体素质,教育行政部门规定学生每天户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制成如图所示中两幅不完整的统计图,请你根据图中提供的信息解答下列问题: (1)、在这次调查中共调查了多少名学生?(2)、求户外活动时间为0.5小时的人数,并补充频数分布直方图;(3)、求表示户外活动时间为2小时的扇形圆心角的度数.25. 节能灯在城市已基本普及,某商场计划购进甲、乙两种节能灯共600只,甲型节能灯进价25元/只,售价30元/只;乙型节能灯进价45元/只,售价60元/只.(1)、要使进货款恰好为 元,甲、乙两种节能灯应各进多少只?(2)、如何进货,商场销售完节能灯时获利恰好是进货价的 ,此时利润为多少元?26. 如图1,点O是弹力墙MN上一点,魔法棒从OM的位置开始绕点O向ON的位置顺时针旋转,当转到ON位置时,则从ON位置弹回,继续向OM位置旋转;当转到OM位置时,再从OM的位置弹回,继续转向ON位置,…,如此反复.按照这种方式将魔法棒进行如下步骤的旋转:第1步,从OA0(OA0在OM上)开始旋转α至OA1;第2步,从OA1开始继续旋转2α至OA2;第3步,从OA2开始继续旋转3α至OA3 , ….例如:当α=30°时,OA1 , OA2 , OA3 , OA4的位置如图2所示,其中OA3恰好落在ON上,∠A3OA4=120°; 当α=20°时,OA1 , OA2 , OA3 , OA4 , OA3的位置如图3所示,中第4步旋转到ON后弹回,即∠A3ON+∠NOA4=80°,而OA5恰好与OA2重合.
(1)、在这次调查中共调查了多少名学生?(2)、求户外活动时间为0.5小时的人数,并补充频数分布直方图;(3)、求表示户外活动时间为2小时的扇形圆心角的度数.25. 节能灯在城市已基本普及,某商场计划购进甲、乙两种节能灯共600只,甲型节能灯进价25元/只,售价30元/只;乙型节能灯进价45元/只,售价60元/只.(1)、要使进货款恰好为 元,甲、乙两种节能灯应各进多少只?(2)、如何进货,商场销售完节能灯时获利恰好是进货价的 ,此时利润为多少元?26. 如图1,点O是弹力墙MN上一点,魔法棒从OM的位置开始绕点O向ON的位置顺时针旋转,当转到ON位置时,则从ON位置弹回,继续向OM位置旋转;当转到OM位置时,再从OM的位置弹回,继续转向ON位置,…,如此反复.按照这种方式将魔法棒进行如下步骤的旋转:第1步,从OA0(OA0在OM上)开始旋转α至OA1;第2步,从OA1开始继续旋转2α至OA2;第3步,从OA2开始继续旋转3α至OA3 , ….例如:当α=30°时,OA1 , OA2 , OA3 , OA4的位置如图2所示,其中OA3恰好落在ON上,∠A3OA4=120°; 当α=20°时,OA1 , OA2 , OA3 , OA4 , OA3的位置如图3所示,中第4步旋转到ON后弹回,即∠A3ON+∠NOA4=80°,而OA5恰好与OA2重合.解决如下问题:
(1)、若α=35°,在图4中借助量角器画出OA2 , OA3 , 其中∠A3OA2的度数是;(2)、若α<30°,且OA4所在的射线平分∠A2OA3 , 在如图5中画出OA1 , OA2 , OA3 , OA4并求出α的值;(3)、若α<30°,且∠A2OA4=20°,求对应的α值.