湖北省咸宁市咸安区2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2021-01-12 类型:期末考试
一、单选题
-
1. 的相反数是( )A、 B、 C、2019 D、-20192. 下列计算正确的是( )A、 B、 C、 D、3. 在 中负数有( )A、1个 B、2个 C、3个 D、4个4. 如图,一个几何体由5个大小相同的正方体搭成,则这个立体图形从左面观察得到的平面图形是( )
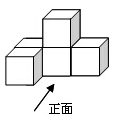 A、
A、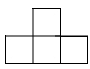 B、
B、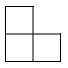 C、
C、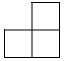 D、
D、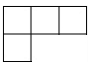 5. 若使 的运算结果最小,则 里应填入的符号是( )A、+ B、- C、× D、÷6. 、 在数轴上的位置如图所示,则下列式子正确的是( )
5. 若使 的运算结果最小,则 里应填入的符号是( )A、+ B、- C、× D、÷6. 、 在数轴上的位置如图所示,则下列式子正确的是( ) A、 B、 C、 D、7. 下列利用等式的性质,错误的是( )A、由 ,得到 B、由 ,得到 C、由 ,得到 D、由 ,得到8. 中国古代人民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果我们设有 辆车,则可列方程( )A、 B、 C、 D、
A、 B、 C、 D、7. 下列利用等式的性质,错误的是( )A、由 ,得到 B、由 ,得到 C、由 ,得到 D、由 ,得到8. 中国古代人民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果我们设有 辆车,则可列方程( )A、 B、 C、 D、二、填空题
-
9. 已知单项式 与 的和是单项式,则 .10. 已知 ,则 .11. 若 是关于 的一元一次方程,则该方程的解 .12. 地球上的海洋面积约三亿六千一百万平方千米,将三亿六千一百万用科学记数法表示为.13. 多项式 与另一个多项式的和为 ,该多项式应为.14. 学校、电影院、公园在平面上的位置分别标为 ,电影院在学校正东,公园在学校的南偏西40°方向,那么 .15. 如图所示,图①是一个三角形,分别连接三边中点得图②,再分别连接图②中的小三角形三边中点,得图③……按此方法继续下去.
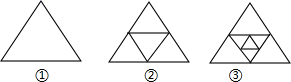
在第 个图形中有个三角形(用含 的式子表示)
16. 下列说法:①连接两点间的线段叫这两点的距离;
②木匠师傅锯木料时,一般先在模板上画出两个点,然后过这两点弹出一条墨线,这样做的原理是:两点之间,线段最短;
③若 三点在同一直线上,且 ,则 是线段 的中点;
④若 ,则有 .
其中一定正确的是(把你认为正确结论的序号都填上) .
三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 先化简,再求值:xy-5(2x2-xy)+2(xy+5x2),其中 , 满足|x-1|+(y+2)2=0.19. 解下列方程:(1)、 ;(2)、 .20. 某公路检修小组从A地出发,在东西方向的公路上检修路面,如果规定向东行驶为正,向西行驶为负,一天行驶记录如下(单位:千米):-5,-3,+6,-7,+9,+8,+4,-2.(1)、求收工时距A地多远;(2)、距A地最远的距离是多少千米?(3)、若每千米耗油0.2升,问这个小组从出发到收工共耗油多少升?21.(1)、平面上有四个点A,B,C,D,按照以下要求作图:
①作直线AD;
②作射线CB交直线AD于点E;
③连接AC,BD交于点F;
(2)、图中共有条线段;(3)、若图中F是AC的一个三等分点,AF<FC,已知线段AC上所有线段之和为18,求AF长.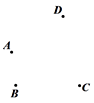 22. 已知直角三角板 和直角三角板 , , , .
22. 已知直角三角板 和直角三角板 , , , .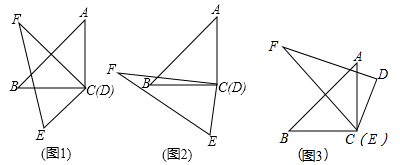 (1)、如图1,将顶点 和顶点 重合,保持三角板 不动,将三角板 绕点 旋转.当 平分 时,求 的度数;(2)、在(1)的条件下,继续旋转三角板 ,猜想 与 有怎样的数量关系?并利用图2所给的情形说明理由;(3)、如图3,将顶点 和顶点 重合,保持三角板 不动,将三角板 绕点 旋转.当 落在 内部时,直接写出 与 的数量关系.23. 2019年元旦,某超市将甲种商品降价30%,乙种商品降价20%开展优惠促销活动.已知甲、乙两种商品的原销售单价之和为2400元,某顾客参加活动购买甲、乙各一件,共付1830元.(1)、甲、乙两种商品原销售单价各是多少元?(2)、若商场在这次促销活动中甲种商品亏损25%,乙种商品盈利25%,那么商场在这次促销活动中是盈利还是亏损了?如果是盈利,求商场销售甲、乙两种商品各一件盈利了多少元?如果是亏损,求销售甲、乙两种商品各一件亏损了多少元?24. (新定义):A、B、C 为数轴上三点,若点 C 到 A 的距离是点 C 到 B 的距离的 3 倍,我们就称点
(1)、如图1,将顶点 和顶点 重合,保持三角板 不动,将三角板 绕点 旋转.当 平分 时,求 的度数;(2)、在(1)的条件下,继续旋转三角板 ,猜想 与 有怎样的数量关系?并利用图2所给的情形说明理由;(3)、如图3,将顶点 和顶点 重合,保持三角板 不动,将三角板 绕点 旋转.当 落在 内部时,直接写出 与 的数量关系.23. 2019年元旦,某超市将甲种商品降价30%,乙种商品降价20%开展优惠促销活动.已知甲、乙两种商品的原销售单价之和为2400元,某顾客参加活动购买甲、乙各一件,共付1830元.(1)、甲、乙两种商品原销售单价各是多少元?(2)、若商场在这次促销活动中甲种商品亏损25%,乙种商品盈利25%,那么商场在这次促销活动中是盈利还是亏损了?如果是盈利,求商场销售甲、乙两种商品各一件盈利了多少元?如果是亏损,求销售甲、乙两种商品各一件亏损了多少元?24. (新定义):A、B、C 为数轴上三点,若点 C 到 A 的距离是点 C 到 B 的距离的 3 倍,我们就称点C 是(A,B)的幸运点.
(1)、(特例感知):如图 1,点A表示的数为﹣1,点 B 表示的数为 3.表示 2 的点 C 到点 A 的距离是 3, 到点 B 的距离是 1,那么点 C 是(A,B)的幸运点.
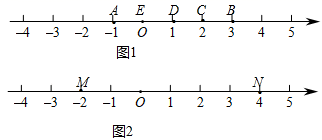
①(B,A)的幸运点表示的数是;
A.﹣1; B.0;C.1;D.2
②试说明 A 是(C,E)的幸运点.
(2)、如图 2,M、N 为数轴上两点,点 M 所表示的数为﹣2,点 N 所表示的数为 4,则(M,N)的幸点示的数为.(3)、(拓展应用):如图 3,A、B 为数轴上两点,点 A 所表示的数为﹣20,点 B 所表示的数为 40.现有一只电子蚂蚁 P 从点 B 出发,以 3 个单位每秒的速度向左运动,到达点 A 停止.当 t 为何值时,P、A 和 B 三个点中恰好有一个点为其余两点的幸运点?
