湖北省随州市广水市2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2021-01-12 类型：期末考试

进入出卷网下载

一、单选题

1. $2019$ 的相反数是（）

A、 $- \frac{1}{2019}$ B、 $\frac{1}{2019}$ C、 $2019$ D、 $- 2019$

查看试题解析
2. 下列计算正确的是（）

A、 $3 x^{2} - x^{2} = 3$ B、 $- 3 a^{2} - 2 a^{2} = - a$ C、 $3 (a - 1) = 3 a - 1$ D、 $- 2 (x + 1) = - 2 x - 2$

查看试题解析
3. 如图，田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能正确解释这一现象的数学知识是（）

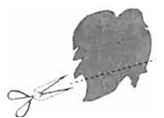A、垂线段最短 B、经过一点有无数条直线 C、两点之间，线段最短 D、经过两点，有且仅有一条直线

查看试题解析
4. 在解方程 $\frac{x - 1}{2} - \frac{2 x + 3}{3}$ ＝1时，去分母正确的是（）

A、3(x﹣1)﹣2(2+3x)＝1 B、3(x﹣1)+2(2x+3)＝1 C、3(x﹣1)+2(2+3x)＝6 D、3(x﹣1)﹣2(2x+3)＝6

查看试题解析
5. 某工程甲单独完成要45天，乙单独完成要30天.若乙先单独干22天，剩下的由甲单独完成，则甲、乙一共用几天可以完成全部工作？设甲、乙一共用x天完成，则符合题意的方程是（）

A、 $\frac{x - 22}{45} + \frac{22}{30} = 1$ B、 $\frac{x + 22}{30} + \frac{22}{45} = 1$ C、 $\frac{x + 22}{45} + \frac{22}{30} = 1$ D、 $\frac{x}{30} + \frac{x - 22}{45} = 1$

查看试题解析
6. 若代数式3x﹣7和6﹣2x互为相反数，则x的值为（）

A、﹣1 B、+1 C、﹣2 D、+2

查看试题解析
7. 下列运用等式的性质，变形正确的是（　　）

A、若x=y，则x﹣5=y+5 B、若a=b，则ac=bc C、若 $\frac{a}{c} = \frac{b}{c}$ ，则2a=3b D、若x=y，则 $\frac{x}{a} = \frac{y}{a}$

查看试题解析
8. 下列说法正确的是（）

A、单项式 $\frac{- 2 x^{2} y}{3}$ 的系数是﹣2，次数是3 B、单项式a的系数是0，次数是0 C、﹣3x²y+3x﹣1是二次三项式 D、单项式 $\frac{- 3^{2} a b}{2}$ 的次数是2，系数是 $- \frac{9}{2}$

查看试题解析
9. 下列说法：
①画一条长为6cm的直线；

②若AC＝BC，则C为线段AB的中点；

③线段AB是点A到点B的距离；

④OC，OD为∠AOB的三等分线，则∠AOC＝∠DOC.

其中正确的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
10. 有理数 $a$ ， $b$ 在数轴上的对应点的位置如图所示，则下列选项正确的是（）

A、 $a + b > 0$ B、 $a + b < 0$ C、 $a - b < 0$ D、 $a - b = 0$

查看试题解析

二、填空题

11. 若 $(a - 1) x^{| a |} + 5 = 0$ 是一元一次方程，则 $a$ 的值为

查看试题解析
12. 我国国土总面积约为 $960$ 万平方公里， $9600000$ 平方公里平方公里.（用科学记数法表示）

查看试题解析
13. 已知 $∠ α = 72 ° 4 8^{'}$ ，则 $∠ α$ 的补角为.

查看试题解析
14. 一个多项式与 $2 x^{2} - x y + 3 y^{2}$ 的和是 $- 2 x y + x^{2} - y^{2}$ ，则这个多项式是．

查看试题解析
15. 某品牌手机的进价为1200元，按原价的八折出售可获利14%，则该手机的原售价为.

查看试题解析
16. 已知∠AOB和∠COD是共顶点的两个角，∠COD的OC边始终在∠AOB的内部，并且∠COD的边OC把∠AOB分为1：2的两个角，若∠AOB＝60°，∠COD＝30°，则∠AOD的度数是.

查看试题解析
17. 解方程:

(1)、 $3 x - 2 (x - 1) = 9 - 4 (x + 3)$

(2)、 $\frac{x + 1}{2} = 3 + \frac{2 - x}{4}$

查看试题解析

三、解答题

18. 计算:

(1)、 $(- 24) \times (\frac{5}{6} - \frac{3}{4} + \frac{1}{2})$

(2)、 ${(- 2)}^{3} + (- \frac{1}{2}) \times [{(- 4)}^{2} - 2^{3}] - {(- 3)}^{2} \div (- 2)$

查看试题解析
19. 先化简，再求值：﹣a²b+（3ab²﹣a²b）﹣2（2ab²﹣a²b），其中|a+1|+(b﹣2)²＝0.

查看试题解析
20. 列方程解应用题.
程大位，明代商人，珠算发明家，被称为珠算之父、卷尺之父.少年时，读书极为广博，对数学颇感兴趣，60岁时完成其杰作《直指算法统宗》（简称《算法统宗》）.

在《算法统宗》里记载了一道趣题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完.试问大、小和尚各多少人？

查看试题解析
21. 已知点O为直线AB上一点，将直角三角板MON的直角顶点放在点O处，并在∠MON内部作射线OC.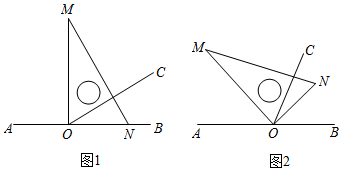

(1)、如图1，三角板的一边ON与射线OB重合，且∠AOC＝150°.若以点O为观察中心，射线OM表示正北方向，求射线OC表示的方向；

(2)、如图2，将三角板放置到如图位置，使OC恰好平分∠MOB，且∠BON＝2∠NOC，求∠AOM的度数；

查看试题解析
22. 为发展校园足球运动，某城区四校决定联合购买一批足球运动装备．市场调查发现：甲、乙两商场以同样的价格出售同种品牌的足球服和足球，已知每套队服比每个足球多50元，两套队服与三个足球的费用相等，经洽谈，甲商场优惠方案是：每购买十套队服，送一个足球；乙商场优惠方案是：若购买队服超过80套，则购买足球打八折．

(1)、求每套队服和每个足球的价格是多少元；

(2)、若城区四校联合购买100套队服和a（a＞10）个足球，请用含a的式子分别表示出到甲商场和乙商场购买装备所花发费用；

(3)、在（2）的条件下，假如你是本次购买任务的负责人，你认为到甲、乙哪家商场购买比较合算？

查看试题解析
23. 我们规定，若关于x的一元一次方程ax=b的解为b﹣a，则称该方程为“差解方程”，例如：2x=4的解为2，且2=4﹣2，则该方程2x=4是差解方程．
请根据上边规定解答下列问题：

(1)、判断3x=4.5是否是差解方程；

(2)、若关于x的一元一次方程6x=m+2是差解方程，求m的值．

查看试题解析
24. 已知数轴上的两点A、B所表示的数分别是a和b，O为数轴上的原点，如果有理数a，b满足 $|a + 8| + {(b - 22)}^{2} = 0$ .

(1)、求a和b的值；

(2)、若点P是一个动点，以每秒5个单位长度的速度从点A出发，沿数轴向右运动，请问经过多长时间，点P恰巧到达线段AB的三等分点？

(3)、若点C是线段AB的中点，点M以每秒3个单位长度的速度从点C开始向右运动，同时点P以每秒5个单位长度的速度从点A出发向右运动，点N以每秒4个单位长度的速度从点B开始向左运动，点P与点M之间的距离表示为PM，点P与点N之间的距离表示为PN，是否存在某一时刻使得PM+PN=12？若存在，请求出此时点P表示的数；若不存在，请说明理由.

查看试题解析