湖北省随州市曾都区2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2021-01-12 类型:期末考试
一、单选题
-
1. -(-2)=( )A、-2 B、2 C、±2 D、42. 单项式 的系数是( )A、4 B、-4 C、 D、-3. 若等式﹣3□2=﹣1成立,则□内的运算符号为( )A、+ B、﹣ C、× D、÷4. 已知等式
 ,
,  为任意有理数,则下列等式不一定成立的是( ) A、
为任意有理数,则下列等式不一定成立的是( ) A、 B、
B、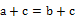 C、
C、 D、
D、 5. 下列去括号中,正确的是( )A、a2-(2a-1)=a2-2a-1 B、a2+(-2a-3)=a2-2a+3 C、3a-[5b-(2c-1)]=3a-5b+2c-1 D、-(a+b)+(c-d)=-a-b-c+d6. 如图,下列说法正确的是( )
5. 下列去括号中,正确的是( )A、a2-(2a-1)=a2-2a-1 B、a2+(-2a-3)=a2-2a+3 C、3a-[5b-(2c-1)]=3a-5b+2c-1 D、-(a+b)+(c-d)=-a-b-c+d6. 如图,下列说法正确的是( )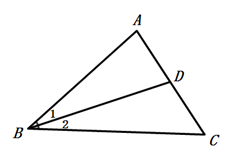 A、∠BCD既可表示成∠ACB,也可以表示成∠C B、以点B为顶点的角有2个,它们是∠1和∠2 C、射线BD是∠ABC的平分线 D、∠BDC与∠BAD互补7. 若 x=-1 是方程 ax+3x=2的解,则 a 的值是( )A、-1 B、5 C、1 D、-58. 如图,马聪同学用剪刀沿虚线将一片平整的银杏叶剪掉一部分,发现剩下的叶片的周长比原叶片的周长要小,能正确解释这一现象的数学知识是( )
A、∠BCD既可表示成∠ACB,也可以表示成∠C B、以点B为顶点的角有2个,它们是∠1和∠2 C、射线BD是∠ABC的平分线 D、∠BDC与∠BAD互补7. 若 x=-1 是方程 ax+3x=2的解,则 a 的值是( )A、-1 B、5 C、1 D、-58. 如图,马聪同学用剪刀沿虚线将一片平整的银杏叶剪掉一部分,发现剩下的叶片的周长比原叶片的周长要小,能正确解释这一现象的数学知识是( ) A、两点确定一条直线 B、经过一点有无数条直线 C、两点之间线段最短 D、两直线相交只有一个交点9. 我们知道,用字母表示的代数式是具有一般意义的,请仔细分析下列赋予4a实际意义的例子:①若a表示一个正方形的边长,则4a表示这个正方形的周长:②若4和a分别表示一个两位数中的十位数和个位数字,则4a表示这个两位数:③一辆汽车的行驶速度是a 千米/小时,则4a表示这辆汽车行驶4小时的路程:④猪肉原价a元/千克,则4a表示按8折优惠买5千克猪肉的金额.其中不正确的是( )A、② B、①② C、②③ D、②④10. 有下列说法:
A、两点确定一条直线 B、经过一点有无数条直线 C、两点之间线段最短 D、两直线相交只有一个交点9. 我们知道,用字母表示的代数式是具有一般意义的,请仔细分析下列赋予4a实际意义的例子:①若a表示一个正方形的边长,则4a表示这个正方形的周长:②若4和a分别表示一个两位数中的十位数和个位数字,则4a表示这个两位数:③一辆汽车的行驶速度是a 千米/小时,则4a表示这辆汽车行驶4小时的路程:④猪肉原价a元/千克,则4a表示按8折优惠买5千克猪肉的金额.其中不正确的是( )A、② B、①② C、②③ D、②④10. 有下列说法:①整数分为正整数和负整数:
②任何数都不等于它的相反数:
③一个数的绝对值越大,表示它在数轴上表示的点离原点越远:
④互为相反数的两个数的同一偶数次方相等:
⑤如果a大于b,那么a的倒数小于b的倒数.
其中正确的个数有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 在国庆70周年联欢晚会上,升起的一面巨幅国旗长为 90米,宽为60米,用科学记数法表示这面国旗的面积为平方米.12. 当x=- 1时,多项式2x2- 3x+ 1的值为.13. 如图,点C是线段AB上的点,点D是线段AC的中点,点E是线段BC的中点,AB = 40, 则线段DE的长为.
 14. 在数轴上,若点P表示﹣2,则距P点3个单位长的点表示的数是.15. 如图是明代数学家程大位的《算法统宗》中的一个问题,其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两(注:明代时1斤= 16两,故有“半斤八两”这个成语.则下列设未知数列方程正确的序号是.
14. 在数轴上,若点P表示﹣2,则距P点3个单位长的点表示的数是.15. 如图是明代数学家程大位的《算法统宗》中的一个问题,其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两(注:明代时1斤= 16两,故有“半斤八两”这个成语.则下列设未知数列方程正确的序号是.
①设这群人人数为x,根据题意得7x- 4=9x+ 8;
②设这群人人数为x,根据题意得7x+ 4= 9x一8;
③设所分银子的数量为x两,根据题意得 =
④设所分银子的数量为x两,根据题意得 =
16. 下列图形由同样的棋子按一定规律组成,图1有3颗棋子,图2有9颗棋子,图3有18颗棋子,图6有颗棋子,图n有颗棋子(用含n的式子表示).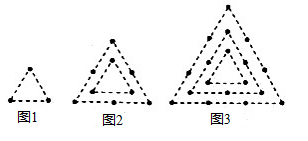
三、解答题
-
17. 计算或化简:(1)、计算:(-2)× ÷(- )×4+(- 2)3;(2)、计算:(-1)2019-(1- )÷3×[3-(-3)2];(3)、化简:4a2-2(a2-b2)-3(a2+b2).18. 按要求解下列各题:(1)、先化简,再求值:5(a2b + 2ab2)- 2(3a2b + 4ab2-1),其中|a-2|+(b+ 3)2= 0:(2)、解方程: =1- .19. 已知平面上点A,B,C,D.按下列要求画出图形:

( 1 )作直线AB,射线CB:
( 2 )连接AD并反向延长至点E,使得AE=AD.
20. 随着手机微信的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来 的销售模式,实行了网上销售.刚大学毕业的小聪把自家的冬枣产品也放到了网上,他原 计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表 是某周的销售情况(超额记为正,不足记为负,单位:斤):星期
一
二
三
四
五
六
日
与计划量的差值
+4
-3
-5
+14
-9
+21
-6
(1)、根据记录的数据可知前三天共卖斤:销售量最多的一天比销售量最少的一天多销售斤;(2)、本周实际销售总量达到了计划数量没有?请通过计算加以说明;(3)、若冬枣每斤按8元出售,每斤冬枣的运费平均3元,那么小聪本周一共收入多少元?21. 如图,点A,O,E在同一条直线上,∠BOD= 90°,OD是∠COE的角平分线,找出图中与∠DOE互余的角.甲、乙、丙三个同学的答案如下:甲:只有一个角,是∠AOB:
乙:有两个角,是∠AOB和∠BOC:
丙:有三个角,是∠AOB,∠BOC,∠COD.
 (1)、请你判断哪个同学的答案是正确的?(2)、请你说明正确答案的理由.22. 甲、乙两家体有用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元,现两家商店搞促销活动.甲店的优惠办法是:每买一副乒乓球拍赠盒乒乓球:乙店的优惠办法是:按定价的9折出售,某班需购买兵乓球拍4副,乒乓球若干(不少于4盒).(1)、用代数式表示(所填代数式需化简):当购买兵乓球的盒数为x盒时,在甲店购买需付款元,在乙店购买需付款元:(2)、若只能选择到一家商店购买, 当购买乒乓球盒数为10盒时,到哪家商店购买比较合算?说出你的理由:(3)、若只能选择到一家商店购买,当购买乒乓球多少盒时,到两家商店所花费用一样多?(4)、若只能选择到一家商店购买,结合(2)(3)的结论,请你回答当购买兵乓球的盒数在什么范围时,到乙商店购买合算.23. 对于有理数a,b,定义两种新运算“※”与“◎”,规定: a※b=a2+2ab,a◎b=|a+b|-|a-b|,例如,2※(-1)=22+2×2×(-1)=0,(-2)※3=|-2+3|-| - 2-3|= -4. b c(1)、计算(-3)※2的值;(2)、若a,b在数轴上的位置如图所示,化简a◎b;
(1)、请你判断哪个同学的答案是正确的?(2)、请你说明正确答案的理由.22. 甲、乙两家体有用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元,现两家商店搞促销活动.甲店的优惠办法是:每买一副乒乓球拍赠盒乒乓球:乙店的优惠办法是:按定价的9折出售,某班需购买兵乓球拍4副,乒乓球若干(不少于4盒).(1)、用代数式表示(所填代数式需化简):当购买兵乓球的盒数为x盒时,在甲店购买需付款元,在乙店购买需付款元:(2)、若只能选择到一家商店购买, 当购买乒乓球盒数为10盒时,到哪家商店购买比较合算?说出你的理由:(3)、若只能选择到一家商店购买,当购买乒乓球多少盒时,到两家商店所花费用一样多?(4)、若只能选择到一家商店购买,结合(2)(3)的结论,请你回答当购买兵乓球的盒数在什么范围时,到乙商店购买合算.23. 对于有理数a,b,定义两种新运算“※”与“◎”,规定: a※b=a2+2ab,a◎b=|a+b|-|a-b|,例如,2※(-1)=22+2×2×(-1)=0,(-2)※3=|-2+3|-| - 2-3|= -4. b c(1)、计算(-3)※2的值;(2)、若a,b在数轴上的位置如图所示,化简a◎b; (3)、若(-2)※x=2◎(-4)+3x,求x的值:(4)、对于任意有理数m,n,请你定义一种新运算“★”,使得(-3)★5=4,直接写出你定义的运算:m★n=(用含m,n的式子表示).24. 如图,点A,B在直线1上,AB = 20cm,∠BAC= 120°.
(3)、若(-2)※x=2◎(-4)+3x,求x的值:(4)、对于任意有理数m,n,请你定义一种新运算“★”,使得(-3)★5=4,直接写出你定义的运算:m★n=(用含m,n的式子表示).24. 如图,点A,B在直线1上,AB = 20cm,∠BAC= 120°. (1)、点P从A出发,沿射线AB以每秒2cm的速度向右运动,同时点Q从B出发,沿射线BA以每秒lcm的速度向左运动,求点P出发多少秒时与点Q重合?(2)、在(1)的条件下,求点P出发多少秒时与点Q相距5cm?(3)、点M为射线AC上一点,AM = 4cm,现将射线AC绕点A以每秒30°的速度顺时针旋转一周后停止,同时点N从点B出发沿直线AB向左运动,在这一运动过程中,是否存在某一时刻,使得点N为BM的中点?若存在,求出点N运动的速度:若不存在,请说明理由.
(1)、点P从A出发,沿射线AB以每秒2cm的速度向右运动,同时点Q从B出发,沿射线BA以每秒lcm的速度向左运动,求点P出发多少秒时与点Q重合?(2)、在(1)的条件下,求点P出发多少秒时与点Q相距5cm?(3)、点M为射线AC上一点,AM = 4cm,现将射线AC绕点A以每秒30°的速度顺时针旋转一周后停止,同时点N从点B出发沿直线AB向左运动,在这一运动过程中,是否存在某一时刻,使得点N为BM的中点?若存在,求出点N运动的速度:若不存在,请说明理由.