湖北省十堰市房县2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2021-01-12 类型:期末考试
一、单选题
-
1. 如果上升8℃记作+8℃,那么﹣5℃表示( )A、上升5℃ B、下降5℃ C、上升3℃ D、下降3℃2. 国内生产总值(GDP)是指按市场价格计算的一个国家(或地区)所有常驻单位在一定时期内生产活动的最终成果,常被公认为衡量国家经济状况的最佳指标,它反映了一国(或地区)的经济实力和市场规模。2019年11月22日,国家统计局发布了《国家统计局关于修订2018年国内生产总值数据的公告》.修订后主要结果为:2018年国内生产总值为近92万亿元.将这个数用科学记数法表示为( )A、9.2×1013 B、9.2×1012 C、92×1012 D、92×10133. 从正面观察如图的两个立体图形,得到的平面图形是( )
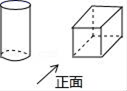 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列运算中,正确的是( )A、5a+3b=8ab B、4a3+2a2=6a5 C、8b2﹣7b2=1 D、6ab2﹣6b2a=05. 下列解方程步骤正确的是( )A、方程5x+6=3x+10可变形为5x﹣3x=10+6 B、方程 =1可变形为 =1 C、方程4(x﹣1)=2(x+5)可变形为4x﹣1=2x+5 D、方程 = ,未知数系数化为1,得t=16. 把夏禹时代的“洛书”用现代数学符号翻译出来就是一个三阶幻方,其实际数学意义就是它的每行、每列、每条对角线上三个数之和均相等,则幻方中a的值是( )
4. 下列运算中,正确的是( )A、5a+3b=8ab B、4a3+2a2=6a5 C、8b2﹣7b2=1 D、6ab2﹣6b2a=05. 下列解方程步骤正确的是( )A、方程5x+6=3x+10可变形为5x﹣3x=10+6 B、方程 =1可变形为 =1 C、方程4(x﹣1)=2(x+5)可变形为4x﹣1=2x+5 D、方程 = ,未知数系数化为1,得t=16. 把夏禹时代的“洛书”用现代数学符号翻译出来就是一个三阶幻方,其实际数学意义就是它的每行、每列、每条对角线上三个数之和均相等,则幻方中a的值是( )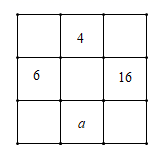 A、6 B、12 C、18 D、247. 如图,小军同学用小刀沿虚线将一半圆形纸片剪掉右上角,发现剩下图形的周长比原半圆形的周长要小,能正确解释这一现象的数学知识是( )
A、6 B、12 C、18 D、247. 如图,小军同学用小刀沿虚线将一半圆形纸片剪掉右上角,发现剩下图形的周长比原半圆形的周长要小,能正确解释这一现象的数学知识是( )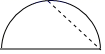 A、经过两点有且只有一条直线 B、经过一点有无数条直线 C、两点之间,线段最短 D、部分小于总体8. 如图,点C,D,E是线段AB上的三个点,下面关于线段CE的表示,其中正确的个数是( )
A、经过两点有且只有一条直线 B、经过一点有无数条直线 C、两点之间,线段最短 D、部分小于总体8. 如图,点C,D,E是线段AB上的三个点,下面关于线段CE的表示,其中正确的个数是( )①CE=CD+DE;②CE=CB﹣EB;③CE=CB﹣DB;④CE=AD+DE﹣AC.
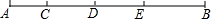 A、1个 B、2个 C、3个 D、4个9. 下列图形(包括数)按照一定的规律排列,依此规律,第300个图形是( )
A、1个 B、2个 C、3个 D、4个9. 下列图形(包括数)按照一定的规律排列,依此规律,第300个图形是( ) ....A、
....A、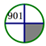 B、
B、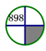 C、
C、 D、
D、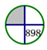 10. 有理数a,b在数轴上的位置如图所示,则下列式子错误的是( )
10. 有理数a,b在数轴上的位置如图所示,则下列式子错误的是( )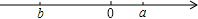 A、ab<0 B、a+b<0 C、|a|<|b| D、a﹣b<|a|+|b|
A、ab<0 B、a+b<0 C、|a|<|b| D、a﹣b<|a|+|b|二、填空题
-
11. 当x时,式子x+1与2x+5的值互为相反数.12. 若a=-2×32 , b=(-2×3)2 , c=-(2×3)2 , 将a,b,c三个数用“<”连接起来应为.13. 《九章算术》中记载:“今有人共买鸡,人出九,盈十一:人出六,不足十六.问人数、鸡价各几何?”译文:“假设有几个人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱,问:有几个人共同出钱买鸡?鸡的价钱是多少?”设有 个人共同买鸡,根据题意列一元一次方程.14. 用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2﹣2ab+b.如:2☆(﹣3)=2×(﹣3)2﹣2×2×(﹣3)+(﹣3)=27.依据此定义化简(1﹣3x)☆(﹣4)=.15. 在同一平面内利用一副三角板,可以直接画出的除三角板本身角的度数以外且小于平角的角度有(例举四个即可).16. 在6,﹣5,﹣4,3四个数中任取两数相乘,积记为A,任取两数相除,商记为B,则A﹣B的最大值为.
三、解答题
-
17. 计算:(-2)2÷(-1 )×0.75×|-2 |+23.18. 已知代数式3(x2-2xy + y2) -2(x2-4xy + y2),先化简,后求值,其中x=-1,y= .19. 解方程: .20. 快递配送员王叔叔一直在一条南北走向的街道上送快递,如果规定向北为正,向南为负,某天他从出发点开始所行走的路程记录为(长度单位:千米):+3,﹣4,+2.+3.﹣1,﹣1,﹣3(1)、这天送完最后一个快递时,王叔叔在出发点的什么方向,距离是多少?(2)、如果王叔叔送完快递后,需立即返回出发点,那么他这天送快递(含返回)共耗油多少升(已知每千米耗油0.2升)?21. 按下列要求画图,并回答问题.
如图,已知∠ABC.
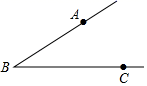 (1)、在射线BC上戳取BD=BA,连接AD;(2)、画∠ABD的平分线交线段AD于点M.
(1)、在射线BC上戳取BD=BA,连接AD;(2)、画∠ABD的平分线交线段AD于点M.回答问题:线段AM和线段DM的大小关系是:AMDM.∠AMB的度数为度.(精确到1度).
(友情提醒:截取用圆规,并保留痕迹:画完图要下结论)
22. 当涂大青山有较为丰富的毛竹资源,某企业已收购毛竹110吨,根据市场信息,将毛竹直接销售,每吨可获利100元;如果对毛竹进行粗加工,每天可加工8吨,每吨可获利1000元;如果进行精加工,每天可加工 吨,每吨可获利5000元,由于受条件限制,在同一天中只能采用一种方式加工,并且必须在一个月(30天)内将这批毛竹全部销售、为此研究了两种方案:(1)、方案一:将收购毛竹全部粗加工后销售,则可获利元;方案二:30天时间都进行精加工,未来得及加工的毛竹,在市场上直接销售,则可获利元.
(2)、是否存在第三种方案,将部分毛竹精加工,其余毛竹粗加工,并且恰好在30天内完成?若存在,求销售后所获利润;若不存在,请说明理由.23. (问题背景)在一条直线上有n个点(n≥2),每两个点确定一条线段,一共有多少条线段?(请在答题卡上按照序号顺序解决问题)(1)、(探究)当仅有2个点时,有 =1条线段;当有3个点时,有 =3条线段;
当有4个点时,有 =6条线段;
①当有5个点时,有条线段;
……
②当有n个点时,从这些点中任意取一点,如图,以这个点为端点和其余各点能组成(n-1)条线段,这样总共有n(n-1)条线段.在这些线段中每条线段都重复了两次,如:线段A1A2和A2A1是同一条线段,所以,一条直线上有n个点,一共有Sn=条线段.
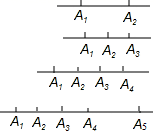 (2)、(应用)
(2)、(应用)③在一条直线上有10个点,直线外一点分别与这10个点连接成线段,一共可以组成个三角形.
④平面上有50个点,且任意三个点不在同一直线上,过这些点作直线,一共能作出条不同的直线.
(3)、(拓展)平面上有n(n≥3)个点,任意三个点不在同一直线上,过任意三点作三角形,一共能作出多少个不同的三角形?当有3个点时,可作1个三角形;
⑤当有4个点时,可作个三角形;
⑥当有5个点时,可作个三角形;
……
⑦当有n个点时,可连成个三角形.
24. 如图,已知O是直线AB上一点,∠BOC<90°,三角板(MON)的直角顶点落在点O处现将三角板绕着点O旋转,并保持OM和OC在直线AB的同一侧.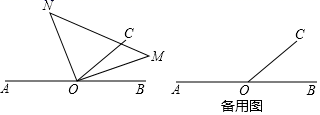 (1)、若∠BOC=50°
(1)、若∠BOC=50°①当OM平分∠BOC时,求∠AON的度数.
②当OM在∠BOC内部,且∠AON=3∠COM时,求∠CON的度数:
(2)、当∠COM=2∠AON时,请画出示意图,猜想∠AOM与∠BOC的数量关系,并说明理由.25. 数轴上点A表示的数为10,点M,N分别以每秒a个单位长度、每秒b个单位长度的速度沿数轴运动,a,b满足|a-3|+(b-4)2=0.
 (1)、请直接写出a= , b=;(2)、如图1,若点M从A出发沿数轴向左运动,到达原点后立即返回向右运动;同时点N从原点O出发沿数轴向左运动,运动时间为t,点P为线段ON的中点.若MP=MA,求t的值;(3)、如图2,若点M从原点向右运动,同时点N从原点向左运动,运动时间为t.当以M,N,O,A为端点的所有线段的长度和为94时,求此时点M对应的数.
(1)、请直接写出a= , b=;(2)、如图1,若点M从A出发沿数轴向左运动,到达原点后立即返回向右运动;同时点N从原点O出发沿数轴向左运动,运动时间为t,点P为线段ON的中点.若MP=MA,求t的值;(3)、如图2,若点M从原点向右运动,同时点N从原点向左运动,运动时间为t.当以M,N,O,A为端点的所有线段的长度和为94时,求此时点M对应的数.