湖北省潜江市2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2021-01-12 类型:期末考试
一、单选题
-
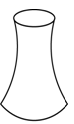
1. 鼓是中国传统民族乐器.作为一种打击乐器,在我国民间被广泛流传,它发音脆亮,独具魅力.除了作为乐器外,鼓在古代还用来传播信息.如图1是我国某少数民族的一种鼓的轮廓图,如果从上面看是图形( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 生产厂家检测4个篮球的质量,结果如图所示,超过标准质量的克数记为正数,不足标准质量的克数记为负数,其中最接近标准质量的篮球是( )A、
2. 生产厂家检测4个篮球的质量,结果如图所示,超过标准质量的克数记为正数,不足标准质量的克数记为负数,其中最接近标准质量的篮球是( )A、 B、
B、 C、
C、 D、
D、 3. 数轴是数形结合思想的产物.有了数轴以后,可以用数轴上的点直观地表示有理数,这样就建立起了“数”与“形”之间的联系.同时,数轴也是我们研究相反数、绝对值的直观工具.有理数a,b,c在数轴上的位置如图所示,则a的相反数是( )
3. 数轴是数形结合思想的产物.有了数轴以后,可以用数轴上的点直观地表示有理数,这样就建立起了“数”与“形”之间的联系.同时,数轴也是我们研究相反数、绝对值的直观工具.有理数a,b,c在数轴上的位置如图所示,则a的相反数是( ) A、a B、b C、c D、﹣b4. 观察算式(-4)× ×(-25)×14,在解题过程中,能使运算变得简便的运算律是( )A、乘法交换律 B、乘法结合律 C、乘法交换律、结合律 D、乘法对加法的分配律5. 已知x=﹣2是方程x+4a=10的解,则a的值是( )A、3 B、
A、a B、b C、c D、﹣b4. 观察算式(-4)× ×(-25)×14,在解题过程中,能使运算变得简便的运算律是( )A、乘法交换律 B、乘法结合律 C、乘法交换律、结合律 D、乘法对加法的分配律5. 已知x=﹣2是方程x+4a=10的解,则a的值是( )A、3 B、 C、2
D、﹣3
6. 李老师用长为 的铁丝做了一个长方形教具,其中一边长为 ,则其邻边长为( )A、 B、 C、 D、7. 如果|a+2|+(b-1)2=0.那么代数式(a+b)2019的值为( )A、3 B、-3 C、1 D、-18. 如图,是一副特制的三角板,用它们可以画出一些特殊角,下列5个角: , , , , ,能用这副特制三角板画出的角有( )
C、2
D、﹣3
6. 李老师用长为 的铁丝做了一个长方形教具,其中一边长为 ,则其邻边长为( )A、 B、 C、 D、7. 如果|a+2|+(b-1)2=0.那么代数式(a+b)2019的值为( )A、3 B、-3 C、1 D、-18. 如图,是一副特制的三角板,用它们可以画出一些特殊角,下列5个角: , , , , ,能用这副特制三角板画出的角有( ) A、5个 B、4个 C、3个 D、2个9. 中国古代人民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果我们设有 辆车,则可列方程( )A、 B、 C、 D、10. 根据以下图形变化的规律,第123个图形中黑色正方形的数量是( ).
A、5个 B、4个 C、3个 D、2个9. 中国古代人民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果我们设有 辆车,则可列方程( )A、 B、 C、 D、10. 根据以下图形变化的规律,第123个图形中黑色正方形的数量是( ). A、182个 B、183个 C、184个 D、185个
A、182个 B、183个 C、184个 D、185个二、填空题
-
11. 过度包装既浪费资源又污染环境.据测算,如果全国每年减少十分之一的包装纸用量,那么能减少3120000吨二氧化碳的排放量.把数据3120000用科学记数法表示为 .12. 如图,在灯塔O处观测到轮船A位于北偏西55°的方向,同时轮船B在南偏东15°的方向,那么∠AOB=°.
 13. 古代埃及人在进行分数运算时,只使用分子是1的分数,因此这种分数也叫做埃及分数.我们注意到,某些真分数恰好可以写成两个埃及分数的和,例如: .
13. 古代埃及人在进行分数运算时,只使用分子是1的分数,因此这种分数也叫做埃及分数.我们注意到,某些真分数恰好可以写成两个埃及分数的和,例如: .( 1 )请将 写成两个埃及分数的和的形式;
( 2 )若真分数 可以写成两个埃及分数和的形式,请写出两个x不同的取值.
14. 已知数轴上三点M,O,N对应的数分别是-1,0,3,点P为数轴上任意点,其对应的数为x.如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时P点到点M、点N的距离相等,则t的值为.
三、解答题
-
15. 计算:(1)、(2)、(3)、16. 如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
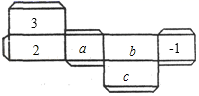 (1)、填空: , , ;(2)、先化简, 再求值: .17. 解方程(1)、(2)、18. 按要求画图:
(1)、填空: , , ;(2)、先化简, 再求值: .17. 解方程(1)、(2)、18. 按要求画图: (1)、如图1平面上有五个点 ,按下列要求画出图形.
(1)、如图1平面上有五个点 ,按下列要求画出图形.①连接 ;
②画直线 交 于点 ;
③画出线段 的反向延长线;
④请在直线 上确定一点 ,使 两点到点 的距离之和最小,并写出画图的依据.
(2)、有5个大小一样的正方形制成如图2所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注意:只需添加一个符合要求的正方形,并用阴影表示)19. 某校七年级 班有 人, 班比 班人数的2倍少8人,如果从 班调出6人到 班.(1)、用代数式表示两个班共有多少人?(2)、用代数式表示调动后, 班人数比 班人数多几人?(3)、 等于多少时,调动后两班人数一样多?20. 如图,已知∠AOC:∠BOC=1:4,OD平分∠AOB , 且∠COD=36°,求∠AOB的度数. 21. 如图1,线段AB=10,点C,E,F在线段AB上.
21. 如图1,线段AB=10,点C,E,F在线段AB上. (1)、如图2,当点E,点F是线段AC和线段BC的中点时,求线段EF的长;
(1)、如图2,当点E,点F是线段AC和线段BC的中点时,求线段EF的长; (2)、当点E,点F是线段AB和线段BC的中点时,请你写出线段EF与线段AC之间的数量关系并简要说明理由.
(2)、当点E,点F是线段AB和线段BC的中点时,请你写出线段EF与线段AC之间的数量关系并简要说明理由. 22. 有一些相同的房间需要粉刷墙面.一天3名一级技工去粉刷8个房间,结果其中有50m2墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40m2墙面.每名一级技工比二级技工一天多粉刷12m2墙面,求一个一级技工和一个二级技工每天粉刷的墙面各是多少.23. 对于任意四个有理数 ,可以组成两个有理数对 与 .
22. 有一些相同的房间需要粉刷墙面.一天3名一级技工去粉刷8个房间,结果其中有50m2墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40m2墙面.每名一级技工比二级技工一天多粉刷12m2墙面,求一个一级技工和一个二级技工每天粉刷的墙面各是多少.23. 对于任意四个有理数 ,可以组成两个有理数对 与 .我们规定: .
例如: .
根据上述规定解决下列问题:
(1)、有理数对 ;(2)、若有理数对 ,则 ;(3)、当满足等式 的 是整数时,求整数 的值.24. 如图,点O是直线AB上的一点,OD⊥OC,过点O作射线OE平分∠BOC. (1)、如图1,如果∠AOC=50°,依题意补全图形,写出求∠DOE度数的思路(不需要写出完整的推理过程);(2)、当OD绕点O顺时针旋转一定的角度得到图2,使得直角边OC在直线AB的上方,若∠AOC=α,其他条件不变,依题意补全图形,并求∠DOE的度数(用含α的代数式表示);(3)、当OD绕点O继续顺时针旋转一周,回到图1的位置,在旋转过程中你发现∠AOC与∠DOE(0°≤∠AOC≤180°,0°≤∠DOE≤180°)之间有怎样的数量关系?请直接写出你的发现.
(1)、如图1,如果∠AOC=50°,依题意补全图形,写出求∠DOE度数的思路(不需要写出完整的推理过程);(2)、当OD绕点O顺时针旋转一定的角度得到图2,使得直角边OC在直线AB的上方,若∠AOC=α,其他条件不变,依题意补全图形,并求∠DOE的度数(用含α的代数式表示);(3)、当OD绕点O继续顺时针旋转一周,回到图1的位置,在旋转过程中你发现∠AOC与∠DOE(0°≤∠AOC≤180°,0°≤∠DOE≤180°)之间有怎样的数量关系?请直接写出你的发现.