湖北省黄冈市麻城市2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2021-01-12 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣3的相反数是（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{3}$ C、 $- 3$ D、 $3$

查看试题解析
2. $a$ ， $b$ ， $c$ 的大小关系如图所示，则 $\frac{a - b}{∣ a - b ∣} - \frac{b - c}{∣ b - c ∣} + \frac{c - a}{∣ c - a ∣}$ 的值是（）

A、 $- 3$ B、 $- 1$ C、 $1$ D、 $3$

查看试题解析
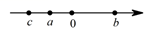3. 如图是由5个相同的小正方体组成的立体图形，这个立体图形的俯视图是（）

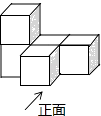A、 B、 C、 D、

查看试题解析
4. 下列各组数中，数值相等的是（）

A、 $3^{2}$ 和 $2^{3}$ B、 $- {(3 \times 2)}^{2}$ 和 $- 3 \times 2^{2}$ C、 $- 4^{2}$ 和 ${(- 4)}^{2}$ D、 $- 2^{3}$ 和 ${(- 2)}^{3}$

查看试题解析
5. 下列合并同类项的结果正确的是（）

A、2x²+3x²＝5x⁴ B、 $3 x + 2 y = 5 x y$ C、7x²﹣4x²＝3 D、9a²b﹣9ba²＝0

查看试题解析
6. 若一个锐角的余角比这个角大 $30^{\circ}$ ，则这个锐角的补角是（）

A、 $30^{\circ}$ B、 $60^{\circ}$ C、 $150^{\circ}$ D、 $155^{\circ}$

查看试题解析
7. 若关于x，y的单项式﹣x^myⁿ^﹣1与mx²y³的和仍是单项式，则m﹣2n的值为（）

A、0 B、﹣2 C、﹣4 D、﹣6

查看试题解析
8. 某商人在一次买卖中均以120元卖出两件衣服，一件赚25%，一件赔25%，在这次交易中，该商人( )

A、赚16元 B、赔16元 C、不赚不赔 D、无法确定

查看试题解析

二、填空题

9. 已知 $a$ 、b互为相反数，m、n互为倒数，x的绝对值为2 ，则 $- 2 m n + \frac{a + b}{m - n} - x^{2}$ =.

查看试题解析
10. 单项式 $\frac{3 a^{2} b}{5}$ 的系数是.

查看试题解析
11. 计算 $33^{\circ} 5 2^{'} + 21^{\circ} 5 4^{'} =$ .

查看试题解析
12. 若要使图中的平面展开图折叠成正方体后，相对面上的两个数之和为6，则 $x + y + z$ 的值为.

查看试题解析
13. 北京西站和北京南站是北京的两个铁路客运中心，如图，A，B，C分别表示天安门、北京西站、北京南站，经测量，北京西站在天安门的南偏西77°方向，北京南站在天安门的南偏西18°方向.则∠BAC=°.

查看试题解析

14. 检查

5

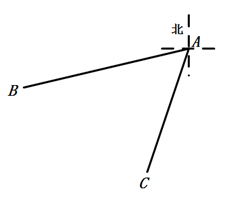个篮球的质量，把超过标准质量的克数记作正数，不足的克数记作负数，检查结果如表：

篮球球的编号	1	2	3	4	5
与标准质量的差（g）	+4	+7	-3	-8	+9

则最接近标准质量的是号篮球；

查看试题解析

15. 已知多项式 $- \frac{1}{3} x^{2} y^{m + 1} + x y^{2} - 3 x^{3} - 6$ 是五次四项式，单项式 $0.4 x^{2 n} y^{5 - m}$ 的次数与这个多项式的次数相同，则 $n =$ .

查看试题解析
16. 一项工程，甲单独做 $10$ 天可以完成，乙单独做 $15$ 天可以完成，甲队先做两天，余下的工程由两队合做 $x$ 天可以完成，则由题意可列出的方程是.

查看试题解析

三、解答题

17. 计算：

(1)、 $- 1 - (1 + 0.5) \times | - \frac{1}{3} | \div (- 4)$ ；

(2)、 $- 3^{2} - 8 \times {(98 - 100)}^{3} - {(- 1)}^{8}$ .

查看试题解析
18. 化简：

(1)、 $(5 a^{2} + 2 a - 1) - 4 [3 - 2 (4 a + a^{2})]$ .

(2)、 $3 x^{2} - [7 x - (4 x - 3) - 2 x^{2}]$ .

查看试题解析
19. 小王购买了一套一居室，他准备将房子的地面铺上地砖，地面结构如图所示，根据图中所给的数据（单位：米），解答下列问题：

(1)、用含 $m ， n$ 的代数式表示地面的总面积 $S$ ；

(2)、已知 $n = 1.5$ ，且客厅面积是卫生间面积的 $8$ 倍，如果铺 $1$ 平方米地砖的平均费用为 $100$ 元，那么小王铺地砖的总费用为多少元?

查看试题解析
20. 解方程：

(1)、2（x﹣2）﹣（1﹣3x）＝x+3；

(2)、 $\frac{2 x - 1}{3}$ ﹣x＝ $\frac{2 x + 1}{4}$ ﹣1.

查看试题解析
21. 如图，点 $C$ 在线段 $A B$ 的延长线上，且 $B C = 2 A B$ ， $D$ 是 $A C$ 的中点，若 $A B = 2 cm$ ，求 $B D$ 的长.

查看试题解析
22. 如图，已知 $∠ 2$ 是 $∠ 1$ 的4倍， $∠ 2$ 的补角比 $∠ 1$ 的余角大 $45 °$ .

(1)、求 $∠ 1$ 、 $∠ 2$ 的度数；

(2)、若 $∠ A O D = 90 °$ ，试问 $O C$ 平分 $∠ A O B$ 吗？请说明理由.

查看试题解析
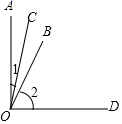23. 我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都可以化为分数形式（整数可看作分母为 $1$ 的分数），那么无限循环小数如何表示为分数形式呢?请看以下示例：
例：将 $0. \dot{7}$ 化为分数形式.

由于 $0. \dot{7} = 0.777 \dots$ ，

设 $x = 0.777 \dots, \dots \dots ①$

则 $10 x = 7.777 \dots, \dots \dots ②$

$② - ①$ 得 $9 x = 7$ ，

解得 $x = \frac{7}{9}$ ，于是得 $0. \dot{7} = \frac{7}{9}$ .

同理可得 $0. \dot{3} = \frac{3}{9} = \frac{1}{3}$ ， $1. \dot{4} = 1 + 0. \dot{4} = 1 + \frac{4}{9} = \frac{13}{9}$ .

根据以上阅读，回答下列问题：（以下计算结果均用最简分数表示）

(1)、 $0. \dot{5} =$ ， $5. \dot{8} =$ ；

(2)、将 $0. \dot{2} \dot{3}$ 化为分数形式，写出推导过程；

(3)、试比较 $0. \dot{9}$ 与 $1$ 的大小： $0. \dot{9}$ $1$ （填“ $>$ ”，“ $<$ ”或“ $=$ ”）；

查看试题解析
24. 某学校实行学案式教学，需印制若干份数学学案，印刷厂有甲、乙两种收费方式，甲种方式：收制版费 $6$ 元，每印一份收印刷费 $0.1$ 元；乙种方式：没有制版费，每印一份收印刷费 $0.12$ 元，若数学学案需印刷 $x$ 份.

(1)、填空：按甲种收费方式应收费元；按乙种收费方式应收费元；

(2)、若该校一年级需印 $500$ 份，选用哪种印刷方式合算?

(3)、印刷多少份时，甲、乙两种收费方式一样多?

查看试题解析
25. 数轴上点 $A$ 对应的数为 $a$ ，点 $B$ 对应的数为 $b$ ，且多项式 $x^{3} y - 2 x y + 5$ 的二次项系数为 $a$ ，常数项为 $b$ .

(1)、直接写出： $a =$ ， $b =$ .

(2)、数轴上点 $A$ ， $B$ 之间有一动点 $P$ ，若点 $P$ 对应的数为 $x$ ，试化简 $| 2 x + 4 | + 2 | x - 5 | - | 6 - x |$ .

(3)、若点 $M$ 从点 $A$ 出发，以每秒 $1$ 个单位长度的速度沿数轴向右移动；同时点 $N$ 从点 $B$ 出发，沿数轴以每秒 $2$ 个单位长度的速度向左移动，到达 $A$ 点后立即返回并向右继续移动，经过t秒后， $M$ ， $N$ 两点相距 $1$ 个单位长度，求t的值.

查看试题解析