河南省郑州市八所省示范高中2020-2021学年高一上学期数学期中联考试卷
试卷更新日期:2021-01-11 类型:期中考试
一、单选题
-
1. 集合 ,则 ( )A、 B、 C、 D、2. 已知函数 的图象如下图所示,则函数 的图象为( )
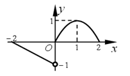 A、
A、 B、
B、 C、
C、 D、
D、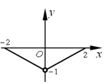 3. 下列四组函数中 与 是同一函数的是( )A、 B、 C、 D、4. 函数 是幂函数,且在 上是减函数,则实数 为( )A、1 B、-1 C、2 D、-1或25. 已知 是一次函数, ,则 的解析式为( )A、 B、 C、 D、6. 若函数 在区间 上存在零点,则常数a的取值范围为( )A、 B、 C、 D、7. 已知 , , ,则( ).A、 B、 C、 D、8. 定义在 上的函数 的图象关于 对称,且 满足:对任意的 , ,且 都有 ,且 ,则关于 的不等式 的解集是( )A、 B、 C、 D、9. 若函数 , 在区间 上是递减函数,则实数 的取值范围为( )A、 B、 C、 D、10. 设方程 的两个根分别为 ,则( )A、 B、 C、 D、11. 已知函数 是 上的减函数,那么 的取值范围是( )A、 B、 C、 D、12. 已知 , , ,当 时,均有 ,则实数 的取值范围是( )A、 B、 C、 D、
3. 下列四组函数中 与 是同一函数的是( )A、 B、 C、 D、4. 函数 是幂函数,且在 上是减函数,则实数 为( )A、1 B、-1 C、2 D、-1或25. 已知 是一次函数, ,则 的解析式为( )A、 B、 C、 D、6. 若函数 在区间 上存在零点,则常数a的取值范围为( )A、 B、 C、 D、7. 已知 , , ,则( ).A、 B、 C、 D、8. 定义在 上的函数 的图象关于 对称,且 满足:对任意的 , ,且 都有 ,且 ,则关于 的不等式 的解集是( )A、 B、 C、 D、9. 若函数 , 在区间 上是递减函数,则实数 的取值范围为( )A、 B、 C、 D、10. 设方程 的两个根分别为 ,则( )A、 B、 C、 D、11. 已知函数 是 上的减函数,那么 的取值范围是( )A、 B、 C、 D、12. 已知 , , ,当 时,均有 ,则实数 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 函数 的最小值为.14. 已知f(x)是定义在R上的偶函数,且f(x+4)=f(x-2).若当x∈[-3,0]时,f(x)=6-x , 则f(919)=.15. 若函数 的定义域为R,则实数 的取值范围是.16. 已知函数 ,若方程 有4个不同的实根 , , , 且 ,则
三、解答题
-
17. 化简下列各式:(1)、 ;(2)、18. 已知集合 , .(1)、若 ,求实数m的取值范围;(2)、若 ,求实数m的取值范围.19. 已知函数 是定义域为 的奇函数,当 时, .
 (1)、求出函数 在R上的解析式;(2)、画出函数 的图象,并根据图象写出 的单调区间.(3)、求使 时的 的值.20. 某学习小组在暑期社会实践活动中,通过对某商店一种商品销售情况的调查发现:该商品在过去的一个月内(以30天计)的日销售价格 (元)与时间 (天)的函数关系近似满足 ( 为正常数).该商品的日销售量 (个)与时间 (天)部分数据如下表所示:
(1)、求出函数 在R上的解析式;(2)、画出函数 的图象,并根据图象写出 的单调区间.(3)、求使 时的 的值.20. 某学习小组在暑期社会实践活动中,通过对某商店一种商品销售情况的调查发现:该商品在过去的一个月内(以30天计)的日销售价格 (元)与时间 (天)的函数关系近似满足 ( 为正常数).该商品的日销售量 (个)与时间 (天)部分数据如下表所示:(天)
10
20
25
30
(个)
110
120
125
120
已知第10天该商品的日销售收入为121元.
(I)求 的值;
(II)给出以下二种函数模型:
① ,② ,
请你根据上表中的数据,从中选择你认为最合适的一种函数来描述该商品的日销售量 与时间 的关系,并求出该函数的解析式;
(III)求该商品的日销售收入 (元)的最小值.
(函数 ,在区间 上单调递减,在区间 上单调递增.性质直接应用.)