四川省成都市2021届高三理数第一次诊断性检测试卷
试卷更新日期:2021-01-11 类型:高考模拟
一、选择题(每小题5分,共12小题,总分60分)
-
1. 设集合A={x|x2-3x-4<0};B={x||x-1|<3,x∈N},则A∩B ( )A、{1,2,3} B、{0,1,2,3} C、{x|x-1<x<4} D、{x|-2<x<4}2. 复数Z= (i为虚数单位),则Z的共轭复数是( )A、-2-i B、-2+i C、2-i D、2+i3. 等比数列{an}满足a2+a3=2,a2-a4=6,则a6=( )A、-32 B、-8 C、8 D、644. 甲乙两台机床同时生产一种零件,10天中,两台机床每天出的次品数分别是:
甲
0
1
0
2
2
0
3
1
2
4
乙
2
2
1
1
1
2
1
1
0
1
, 分别表示甲乙两组数据的平均数,S1 , S2分别表示甲乙两组数据的方差,则下列选项正确的是( )
A、 = ,S1>S2 B、 > ,S1>S2 C、 < ,S1>S2 D、 > ,S1<S25. 若函数f(x)=x3-3x2+a有且仅有一个零点,则实数a的取值范围为( )A、(-∞,0)∪(4,+∞) B、(-∞,-8)∪(0,+∞) C、[0,4] D、(-8,0)6. 若向量a,b满足|a|=2,(a+2b)·a=6,则b在a方向上的投影为( )A、1 B、 C、 D、-17. 设a=log2020 ,b=ln ,c=2021 ,则a,b,c的大小关系是( )A、a>b>c B、a>c>b C、c>a>b D、c>b>a8. 若a,β,γ是空间中三个不同的平面,a∩β=l,a∩γ=m,r∩β=n,则l∥m是n∥m的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件9. 已知平行于x轴的一条直线与双曲线 =1(a>0,b>0)相交于P,Q两点,|PQ|=4a ,∠PQO= (O为坐标原点),则该双曲线的离心率为( )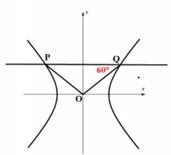 A、 B、 C、 D、10. 已知锐角φ满足 sinφ-cosφ=1,若要得到函数f(x)= -sin2(x+q)的图象,则可已将函数y= sin2x的图象( )A、向左平移 个单位长度 B、向左平移 个单位长度 C、向右平移 个单位长度 D、向右平移 个单位长度11. 已知抛物线x2=4y的焦点为F,过F的直线l与抛物线相交于A,B两点,P(0, )。若PB⊥AB,则|AF|=( )
A、 B、 C、 D、10. 已知锐角φ满足 sinφ-cosφ=1,若要得到函数f(x)= -sin2(x+q)的图象,则可已将函数y= sin2x的图象( )A、向左平移 个单位长度 B、向左平移 个单位长度 C、向右平移 个单位长度 D、向右平移 个单位长度11. 已知抛物线x2=4y的焦点为F,过F的直线l与抛物线相交于A,B两点,P(0, )。若PB⊥AB,则|AF|=( )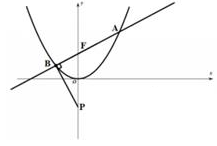 A、 B、2 C、 D、312. 已知函数f(x)=x+ln(x-1),g(x)=xlnx。若f(x)=1+2lnt,g(x2)=t2 , 则(x1x2-x2)lnt的最小值为( )A、 B、 C、- D、-
A、 B、2 C、 D、312. 已知函数f(x)=x+ln(x-1),g(x)=xlnx。若f(x)=1+2lnt,g(x2)=t2 , 则(x1x2-x2)lnt的最小值为( )A、 B、 C、- D、-二、填空题:本大题共4小题,共计20分.
-
13. 7的展开式中x-1的系数是。14. 已知x,y满足约束条件 ,则z=2x-3y的最小值为15. 数列{an}的前n项和为Sn , an+2Sn=3n , 数列{bn}满足3bn= (3an+2-an+1)(n∈N"), 则数列{bn}的前10项和为16. 在三棱锥P-ABC中,PA⊥平面ABC,AB⊥BC,PA=AB=1,AC= 。三棱锥P-ABC的所有顶点都在球O的表面上,则球O的半径为;若点M,N分别是△ABC与△PAC的重心,直线MN与球O的表面相交于D,E两点,则线段DE的长度为。
三、解答题: 本大题共6小题,共计70分.
-
17. 在△ABC中,点M在边AC上,CM = 3MA,tan∠ABM= ,tan∠BMC=(1)、求角A的大小;(2)、若BM= ,求△ABC的面积18. 一网络公司为某贫困山区培养了100名“乡土直播员”,以帮助宣传该山区文化和销售该山区的农副产品,从而带领山区人民早日脱贫致富.该公司将这100名“乡土直播员”中每天直播时间不少于5小时的评为“网红乡土直播员”,其余的评为“乡土直播达人”。根据实际评选结果得到了下面2×2列联表:
网红乡土直播员
乡土直播达人
合计
男
10
40
50
女
20
30
50
合计
30
70
100
附: K2= ,其中n=a+b+c+d
P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
0.005
878'01
K0
2.072
2.706
3.841
5.024
6.635
7.879
I00'0
(1)、根据列联表判断是否有95%的把握认为“网红乡土直播员”与性别有关系?(2)、在“网红乡土直播员”中按分层抽样的方法抽取6人,在这6人中选2人作为“乡土直播推广"大使”.设被选中的2名“乡土直播推广大使”中男性人数为5,求与的分布列和期望。19. 如图,长方体ABCD -A1B1C1D1的底面是边长为2的正方形,AA1=4,点E,F,M,N分别为棱CC1 , BC, BB1 , AA1的中点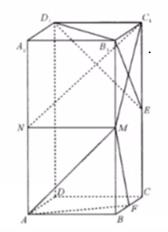 (1)、求证:平面B1D1E⊥平面C1MN.(2)、若平面AFM∩平面A1B1C1D1=l,求直线l与平面B1D1E1所成角的正弦值.20. 已知函数f(x)=(x-2)e*x- x2+ax,a∈R.(1)、讨论函数f(x)的单调性(2)、若不等式f(x)+(x+1)ex+ x2-2ax +a>0恒成立,求a的取值范围.21. 已知椭圆C: =1(a>b>0)的离心率为 , 且直线 =1与圆x2+ y2=2相切.(1)、求椭圆C的方程;(2)、设直线l与椭圆C相交于不同的两点A,B,M为线段AB的中点,O为坐标原点,射线OM与椭圆C 相交于点P,且0点在以4B为直径的圆上。记△AOM,△BOP的面积分别为S1 , S2 , 求 的取值范围.
(1)、求证:平面B1D1E⊥平面C1MN.(2)、若平面AFM∩平面A1B1C1D1=l,求直线l与平面B1D1E1所成角的正弦值.20. 已知函数f(x)=(x-2)e*x- x2+ax,a∈R.(1)、讨论函数f(x)的单调性(2)、若不等式f(x)+(x+1)ex+ x2-2ax +a>0恒成立,求a的取值范围.21. 已知椭圆C: =1(a>b>0)的离心率为 , 且直线 =1与圆x2+ y2=2相切.(1)、求椭圆C的方程;(2)、设直线l与椭圆C相交于不同的两点A,B,M为线段AB的中点,O为坐标原点,射线OM与椭圆C 相交于点P,且0点在以4B为直径的圆上。记△AOM,△BOP的面积分别为S1 , S2 , 求 的取值范围.四、选修4-4:坐标系与参数方程