浙教版备考2021年中考数学一轮复习专题2—— 整式与因式分解
试卷更新日期:2021-01-11 类型:一轮复习
一、单选题
-
1. 下列运算正确的是( )A、2x2+x2=2x4 B、x3x2=2x3 C、(x2)3=x2 D、2x7÷x5=2x22. 计算:(﹣ x2y)3=( )A、﹣2x6y3 B、 x6y3 C、﹣ x6y3 D、﹣ x5y43. 下列等式从左边到右边的变形中,是因式分解的是( )A、a(a+3)=a2+3a B、a2+4a-5=a(a+4)-5 C、(a+2)(a-2)=a2-4 D、a2+6a+9=(a+3)24. 方程 的根为( )A、 B、 C、 或 D、以上都不对5. 下列说法错误的是( )A、 是2个数a的和 B、 是2和数a的积 C、 是单项式 D、 是偶数6. 图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是( )
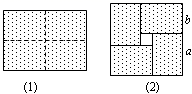 A、 B、 C、 D、7. 已知 , ,那么ab的值为( )A、 B、 C、 D、8. 如图(1),边长为m的正方形剪去边长为n的正方形得到①、②两部分,再把①、②两部分拼接成图(2)所示的长方形,根据阴影部分面积不变,你能验证以下哪个结论( )
A、 B、 C、 D、7. 已知 , ,那么ab的值为( )A、 B、 C、 D、8. 如图(1),边长为m的正方形剪去边长为n的正方形得到①、②两部分,再把①、②两部分拼接成图(2)所示的长方形,根据阴影部分面积不变,你能验证以下哪个结论( ) A、(m﹣n)2=m2﹣2mn+n2 B、(m+n)2=m2+2mn+n2 C、(m﹣n)2=m2+n2 D、m2﹣n2=(m+n)(m﹣n)9. 单项式xm﹣1y3与4xyn的和是单项式,则nm的值是( )A、3 B、6 C、8 D、910. 关于多项式 -3x+1下列说法正确的是( )A、它是二次三项式 B、它的最高次项为 C、它由 、3x和1三项组成 D、三项的次数依次为3、1、111. 下列添括号错误的是 ( )A、
A、(m﹣n)2=m2﹣2mn+n2 B、(m+n)2=m2+2mn+n2 C、(m﹣n)2=m2+n2 D、m2﹣n2=(m+n)(m﹣n)9. 单项式xm﹣1y3与4xyn的和是单项式,则nm的值是( )A、3 B、6 C、8 D、910. 关于多项式 -3x+1下列说法正确的是( )A、它是二次三项式 B、它的最高次项为 C、它由 、3x和1三项组成 D、三项的次数依次为3、1、111. 下列添括号错误的是 ( )A、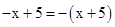 B、
B、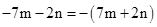 C、
C、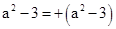 D、
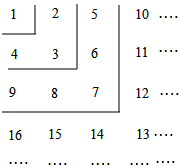
D、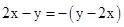 12. 对二次三项式4x2﹣6xy﹣3y2分解因式正确的是( )A、 B、 C、 D、13. 根据图中数字的规律,若第n个图中出现数字396,则 ( )
12. 对二次三项式4x2﹣6xy﹣3y2分解因式正确的是( )A、 B、 C、 D、13. 根据图中数字的规律,若第n个图中出现数字396,则 ( ) A、17 B、18 C、19 D、2014. 一个大正方形内放入两个同样大小的小正方形纸片,按如图1放置,两个小正方形纸片的重叠部分面积为4;按如图2放置(其中一小张正方形居大正方形的正中),大正方形中没有被小正方形覆盖的部分(阴影部分)的面积为44,则把两张小正方形按如图3放置时,两个小正方形重叠部分的面积为( )
A、17 B、18 C、19 D、2014. 一个大正方形内放入两个同样大小的小正方形纸片,按如图1放置,两个小正方形纸片的重叠部分面积为4;按如图2放置(其中一小张正方形居大正方形的正中),大正方形中没有被小正方形覆盖的部分(阴影部分)的面积为44,则把两张小正方形按如图3放置时,两个小正方形重叠部分的面积为( )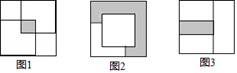 A、10 B、12 C、14 D、16
A、10 B、12 C、14 D、16二、填空题
-
15. 若单项式 与单项式 是同类项,则 .16. 一套运动装标价200元,按标价的八折销售,则这套运动装的实际售价为元.17. 全校学生总数是 ,其中男生占总人数的48%,则女生人数是 .18. 若多项式 是关于x,y的三次多项式,则 .19. 把多项式3a-5a2+6a3-2按a的降幂排列: . 把多项式4x2y-5x3-3xy2+y3按y的升幂排列: .20. 如图,将从1开始的正整数按规律排列,例如:位于第3行、第4列的数是12,则位于第45行、第6列的数是 .
三、综合题
-
21. 先化简,再求值: ,其中a=2.22. 先化简,再求值:(x+1)(x-1)+x(2-x),其中x= .23. 先化简,再求值.(2x+3)(2x﹣3)﹣4x(x﹣1)+(x﹣2)2 , 其中x=﹣ .24. 我们用 来表示不超过实数x的最大整数,如 .(1)、若 ,则实数x所有可能取值的范围是.(2)、求方程 的解.25.(1)、解方程:(2)、化简求值: ,其中26. 指出下列各式中,哪些是单项式、哪些是多项式、哪些是整式?填在相应的横线上:① ;②-x;③ ;④10;⑤6xy+1;⑥ ;⑦ m2n;⑧2x2-x-5;⑨a7;⑩
单项式:;
多项式:;
整式:;
27. 已知M=x2-3,N=4(x— )(1)、当x=-1时,求M-N的值;(2)、当时1<x< 时,试比较M,N的大小.28. 阅读下列材料:( 1 )关于x的方程x2﹣3x+1=0(x≠0)方程两边同时乘以 得:x-3+ =0即x+ =3, , .
( 2 )a3+b3=(a+b)(a2﹣ab+b2);a3﹣b3=(a﹣b)(a2+ab+b2).
根据以上材料,解答下列问题:
(1)、x2﹣4x+1=0(x≠0),则x+ = , = , =;(2)、2x2﹣7x+2=0(x≠0),求 的值.29. 阅读下列材料:分解因式的常用方法有提取公因式法、公式法,但有部分项数多于3的多项式只单纯用上述方法就无法分解,如 ,我们细心观察这个式子就会发现,前三项符合完全平方公式,进行变形后可以与第四项结合再运用平方差公式进行分解.过程如下: ,这种分解因式的方法叫分组分解法.利用这种分组的思想方法解决下列问题:知识运用:
(1)、试用“分组分解法”分解因式: ;(2)、已知a,b,c为△ABC的三边,且 ,试判断△ABC的形状.(3)、已知四个实数a,b,c,d,满足a≠b,c≠d,并且 ,同时成立.①当k=1时,求a+c的值
②当k≠0时,用含有a的代数式分别表示b,c,d(直接写出答案即可)