初中数学北师大版八年级下学期 第一章 单元测试卷
试卷更新日期：2021-01-10 类型：单元试卷
一、单选题
-
1. 等腰三角形的两边长为3和8，则这个等腰三角形的周长是（ ）A、14 B、19 C、14或19 D、202. 如图，DE垂直平分AB.如果AC=5cm，BC=12cm，则△ADC的周长为( ）
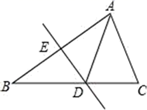A、17cm B、10cm C、15cm D、22cm3. 如图所示，在△ABC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于点D，如果AC=3cm，那么AE+DE等于（ ）
A、2cm B、3cm C、4cm D、5cm4. 如图，∠BAD＝∠BCD＝90°，AB＝CB，据此可以证明△BAD≌△BCD，证明的依据是 （ ）
A、AAS B、ASA C、SAS D、HL5. 如图，在△ABC中，BC=8，AB的垂直平分线分别交AB，AC于点D，E。若△BCE的周长为17，则AC的长为（ ）
A、8 B、9 C、15 D、176. 如图，某商场一楼与二楼之间的电梯示意图. ， 的长是 ，则乘电梯从点 到点 上升的高度h是（ ）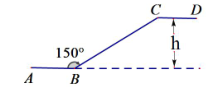
A、 B、 C、 D、7. 在等腰三角形ABC中，∠A=70°，则∠C的度数不可能是（ ）A、40° B、55° C、65° D、70°8. 如图，在△ABC中，AB的垂直平分线交AB于点E，交BC于点D，△ADC的周长为10，且BC-AC=2，则BC的长为（ ）
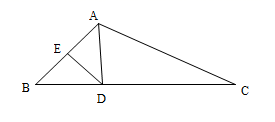A、 B、 C、 D、9. 在 中， ， ，过点B作 ，交 于点D，若 ，则 的长度为（ ）
A、2 B、3 C、4 D、510. 如图，在△ABC中，∠A=60°，BE⊥AC，垂足为E，CF⊥AB，垂足为F，点D是BC的中点，BE，CF交于点M，如果CM=4，FM=5，则BE等于（ ）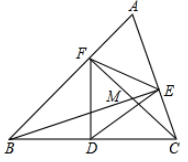
A、14 B、13 C、12 D、11二、填空题
-
11. 如图所示ΔABC中，AB=AC=14cm，AB的垂直平分线MN交AC于D，ΔDBC的周长是24cm，则BC=cm.
12. 如图，在△ABC中，若PM，QN分别垂直平分AB，AC，如果BC=10cm，则△APQ的周长为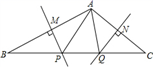
13. 如图，在Rt△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC， DC=4cm，则点D到AB的距离为.
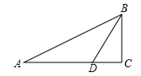14. 如图，ED为△ABC的边AC的垂直平分线，且AB＝5，△BCE的周长为8，则BC＝.
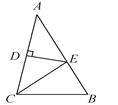15. 等腰三角形一腰上的高与另一腰的夹角为50°，则它的底角等于。16. 在直角坐标系中，O为原点，已知A（1，1），在坐标轴上确定点P，使△AOP为等腰三角形，则符合条件的点P有个．17. 如图，在Rt△ABC中，∠ACB=90°，∠A=30°，CD是斜边AB上的高，若AB=8，则BD= ．
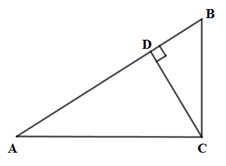18. 如图，点P是∠AOB的角平分线OC上一点，PN⊥OB于点N，点M是线段ON上一点.已知OM＝3，ON＝5，点D为OA上一点，若满足PD＝PM，则OD的长度为.
三、解答题
-
19. 如图，已知 ，垂足分别为点 ，且 ．
求证：
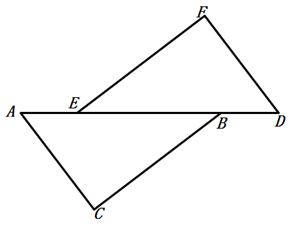20. 如图，在等腰三角形ABC中，AB＝AC，AD是BC边上的中线，∠ABC的平分线BG交AD于点E，EF⊥ AB，垂足为F. 求证：EF＝ED.
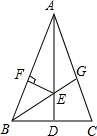21. 如图，已知∠BAC=∠BCA，∠BAE=∠BCD=90°，BE=BD．求证：∠E=∠D．
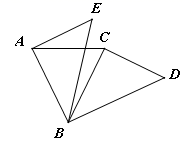22. 如图，在 中， ，求 的长
23. 在一次数学课上，王老师在黑板上画出图（如图所示），并写出四个等式：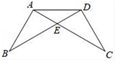
（1）AB＝DC，（2）BE＝CE ， （3）∠B＝∠C ， （4）∠BAE＝∠CDE要求同学从这四个等式中选出两个作为条件，推出△AED是等腰三角形，请你试着完成王老师提出的要求，并说明理由．已知：
求证：△AED是等腰三角形．
24.阅读下列材料，解答问题：
定义：线段AD把等腰三角形ABC分成△ABD与△ACD（如图1），如果△ABD与△ACD均为等腰三角形，那么线段AD叫做△ABC的完美分割线.
(1)、如图1，已知△ABC中，AB=AC，∠BAC=108°，AD为△ABC的完美分割线，且BD<CD，则∠B= ， ∠ADC=.(2)、如图2，已知△ABC中，AB=AC，∠A=36°，BE为△ABC的角平分线，求证：BE为△ABC完美分割线.(3)、如图3，已知△ABC是一等腰三角形纸片，AB=AC，AD是它的一条完美分割线，将△ABD沿直线AD折叠后，点B落在点B1处，AB1交CD于点E，求证：DB1=EC.