人教版数学八年级下册 第十七章 勾股定理 17.2 勾股定理的逆运算 同步练习
试卷更新日期：2021-01-10 类型：同步测试
一、单选题
-
1. 下列四组线段中，可以构成直角角形的是（ ）A、1，1，2 B、1， ，3 C、2，3，4 D、 ，3，42. 下列说法中，正确的有（ ）
①如果 ，那么 是直角三角形；②如果 ，则 是直角三角形；③如果三角形三边之比为 ，则 为直角三角形；④如果三角形三边长分别是 、 、 ，则 是直角三角形．
A、1个 B、2个 C、3个 D、4个3. 下列条件中，不能判断一个三角形是直角三角形的是（ ）A、三条边的比是1∶2∶3 B、三条边满足关系a2=c2－b2 C、三个角的比是1∶2∶3 D、三个角满足关系∠B+∠C=∠A4. 如图，正方形ABCD的面积是（ ）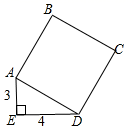
A、5 B、25 C、7 D、15. 小明想知道学校旗杆（垂直地面）的高，他发现旗杆上的绳子垂到地面还多了1m，当他把绳子拉直后，发现绳子下端拉开5m，且下端刚好接触地面，则旗杆的高是（ ）A、6m B、8m C、10m D、12m6. 如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为5m，梯子的顶端B到地面的距离为12m，现将梯子的底端A向外移动到A'，使梯子的底端A'到墙根O的距离等于6m，同时梯子的顶端B下降至B'，那么BB'（ ）
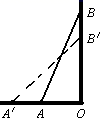A、小于1m B、大于1m C、等于1m D、小于或等于1m7. 勾股定理是人类最伟大的科学发现之一，在我国古代算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大的正方形内．若知道图中阴影部分的面积，则一定能求出（ ）
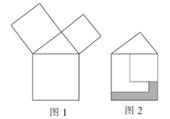A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和8. 如图，点D是正△ABC内的一点，DB=3，DC=4，DA=5，则∠BDC的度数是（ ）
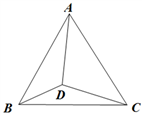A、120° B、135° C、140° D、150°二、填空题
-
9. 已知一个三角形的三边分别是6cm、8cm、10cm ， 则这个三角形的面积是 ．10. 根据下列已知条件，能确定△ABC的大小和形状的是
①AB＝3，BC＝4，AC＝5 ②AB＝4，BC＝3，∠A＝30º
③∠A＝60º，∠B＝45º，AB＝4 ④∠C＝90º，AB＝6，AC=5
11. 如图，已知∠C=90°，AB=12，BC=3，CD=4，AD=13，则∠ABD= ．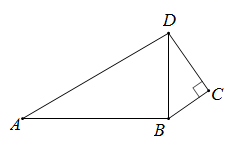
12. 如图，一圆柱体的底面周长为 ，高 为 ， 是直径，一只蚂蚁从点 出发沿着圆柱体的表面爬行到点 的最短路程是 ．
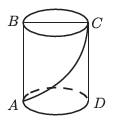13. 如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成．若较短的直角边BC=2.5，将四个直角三角形中较长的直角边分别向外延长一倍，得到图2所示的“数学风车”，若△BCD的周长是15，则这个风车的外围周长是 ．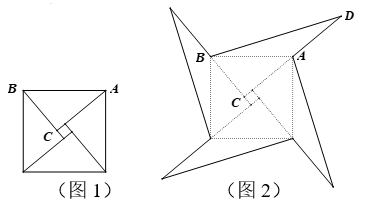
三、解答题
-
14. 如图，在4×4的正方形网格中，每个小正方形的边长都是1，△ABC三个顶点分别在正方形网格的格点上，试判断△ABC是否是直角三角形．
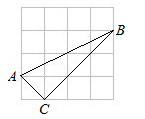15. 如图，四边形ABCD中，AB=20，BC=15，CD=7，AD=24，∠B=90°，求证：∠A+∠C=180°.
16. 如图，四边形ABCD中，AB＝AD，∠BAD＝90°，若AB＝2 ，CD＝4 ，BC＝8，求四边形ABCD的面积．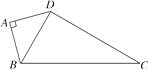
四、综合题
-
17. 已知a、b、c满足|a- |+ +(c-4 )2=0(1)、求a、b、c的值：(2)、判断以a、b、c为边的三角形的形状，并说明理由。18. 如图，在一条东西走向河流的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点H（A、H、B在同一条直线上），并新修一条路CH，测得CB＝1.5千米，CH＝1.2千米，HB＝0.9千米.
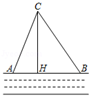(1)、问CH是否为从村庄C到河边的最近路？请通过计算加以说明；(2)、求新路CH比原路CA少多少千米？19. 台风是一种自然灾害，它以台风中心为圆心在周围上百千米的范围内形成极端气候，有极强的破坏力，如图，有一台风中心沿东西方向 由 行驶向 ，已知点 为一海港，且点 与直线 上的两点 ， 的距离分别为 ， ，又 ，以台风中心为圆心周围 以内为受影响区域．
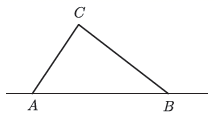(1)、求 的度数．(2)、海港 受台风影响吗？为什么？(3)、若台风的速度为20千米/小时，当台风运动到点 处时，海港 刚好受到影响，当台风运动到点 时，海港 刚好不受影响，即 ，则台风影响该海港持续的时间有多长？