人教版数学八年级下册 第十七章 勾股定理 17.1 勾股定理 同步练习
试卷更新日期：2021-01-10 类型：同步测试
一、单选题
-
1. 如右图：三个正方形和一个直角三角形，图形A的面积是（ ）
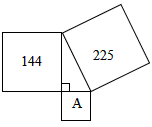A、225 B、144 C、81 D、无法确定2. 如图，AB⊥CD ， △ABD、△BCE都是等腰三角形，如果CD＝8cm ， BE＝3cm ， 那么AC长为（ ）
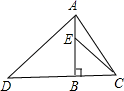A、4cm B、5cm C、8cm D、 cm3. 在Rt△ABC中，∠C=90°，AB=10，BC=8，则AC=（ ）A、4 B、5 C、6 D、74. 如图，长方体的长为 ，宽为 ，高为 ，点 到点 的距离为 ，一只蚂蚁如果要沿着长方体的表面从点 爬到点 ，需要爬行的最短距离是（ ）
A、4 B、5 C、 D、5. 如图，在Rt△ABC中，∠ACB=90°，AC=BC，边AC落在数轴上，点A表示的数是1，点C表示的数是3．以点A为圆心、AB长为半径画弧交数轴负半轴于点B1 ， 则点B1所表示的数是（ ）
A、－2 B、－2
C、1－2
D、2 －1
6. 如图，在波平如镜的湖面上，有一朵盛开的美丽的红莲，它高出水面30cm．突然一阵大风吹过，红莲被吹至一边，花朵下部刚好齐及水面，如果知道红莲移动的水平距离为60cm，则水是（ ）cm．
A、35 B、40 C、50 D、457. 将一根 的筷子，置于底面直径为 ，高 的圆柱形水杯中，如图所示，设筷子露在杯子外面的长度 ，则 的取值范围是（ ）
A、 B、 C、 D、8. 等腰三角形一腰长为5，这一腰上的高为3，则这个等腰三角形底边长为（ ）A、 B、 C、 或 D、 或9. 已知：如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形，若斜边AB=3，则图中阴影部分的面积为（ ）
A、9 B、3 C、 D、10. 如图，在平行四边形 中， ， 是锐角， 于点E，F是 的中点，连接 ；若 ，则 的长为（ ）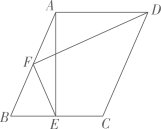
A、2 B、 C、 D、二、填空题
-
11. 如图，在△ABC中，若∠A=30°，∠B=45°，AC= ，则BC=
12. 已知△ABC中，AB=20，AC=15，BC边上的高为12，则△ABC的周长为 ．13. 如图，阴影部分是两个正方形，其它部分是两个直角三角形和一个正方形．若右边的直角三角形 中， ， ，则阴影部分的面积是 ．
14. 一辆装满货物，宽为 2.4m的卡车，欲安全通过如图所示的隧道，则卡车装满货物后的高度必须低于
15. 如图，等腰△ABC中，AB=AC=10，BC=12，AD平分 ，且AD=8，P ， Q分别是AB、AD上的动点，连接BP ， PQ ， 则BP +PQ的最小值为 ．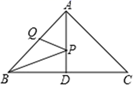
16. 如图是学校艺术馆中的柱子，高4.5m ． 为迎接艺术节的到来，工作人员用一条花带从柱底向柱顶均匀地缠绕3圈，一直缠到起点的正上方为止．若柱子的底面周长是2m ， 则这条花带至少需要m ．
17. 如图，△ABC中，AB＝AC＝5，BC＝6，AD是BC边上的中线，F是AD上的动点，E是AC边上的动点，则CF+EF的最小值为.
三、解答题
-
18. 如图：在△ABC中∠C=90°，AB＝3，BC＝2 ， 求△ABC的面积．
19. 如图，在笔直的高速路旁边有A、B两个村庄，A村庄到公路的距离AC＝8km ， B村庄到公路的距离BD＝14km ， 测得C、D两点的距离为20km ， 现要在CD之间建一个服务区E ， 使得A、B两村庄到E服务区的距离相等，求CE的长．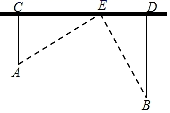
20. 有一个小朋友拿着一根竹竿通过一个长方形的门，如果把竹竿竖放就比门高出1尺，斜入就恰好等于门的对角线长，已知门宽4尺，请求竹竿的长度．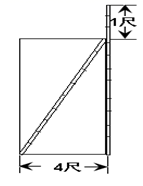
四、综合题
-
21. 如图，把一张长方形纸片ABCD折叠起来，使其对角顶点A与点C重合，点D与点G重合，若BC＝8，AB＝4，求：
(1)、求CF的长．(2)、求EF的长．(3)、求阴影部分△GED的面积．