初中数学北师大版八年级下学期 第一章 1.2 直角三角形
试卷更新日期：2021-01-09 类型：同步测试
一、单选题
-
1. 下列判定直角三角形全等的方法，不正确的是（ ）A、两条直角边对应相等。 B、斜边和一锐角对应相等。 C、斜边和一条直角边对应相等。 D、两锐角相等。2. 如图，DE⊥AC于点E，BF⊥AC于点F，且DE=BF，若利用“HL”证明△DEC≌△BFA，则需添加的条件是（ ）
A、DC=BA B、EC=FA C、∠D=∠B D、∠DCE=BAF3. 如图由于台风的影响，一棵树在离地面 处折断，折断后树干上部分与地面成30度的夹角，折断前长度是 （ ）
A、 B、 C、 D、 .4. 如图，BC⊥AC，BD⊥AD，且BC=BD，可说明三角形全等的方法是（ ）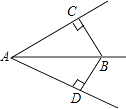
A、SAS B、AAS C、SSA D、HL5. 如图，AC，BD是矩形ABCD的对角线，过点D作DE∥AC交BC的延长线于E，则图中与△ABC全等的三角形共有（ ）
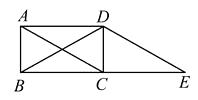A、1个 B、2个 C、3个 D、4个6. 如图，在 中， 是AC上一点， 于点E， 连接BD，若AC=8cm，则 等于（ ）
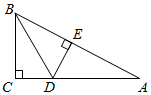A、6cm B、7cm C、8cm D、9cm7. 如图，在△ABC中，∠C＝90°，点E是AC上的点，且∠1＝∠2，DE垂直平分AB，垂足是D，如果EC＝3cm，则AE等于（ ）
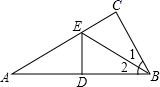A、3cm B、4cm C、6cm D、9cm8. 如图，点E是BC的中点，AB⊥BC，DC⊥BC，AE平分∠BAD，下列结论：①∠AED＝90°；②∠ADE＝∠CDE；③DE＝BE；④AD＝AB＋CD，四个结论中成立的是（ ）
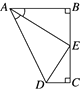A、①②④ B、①②③ C、②③④ D、①③二、填空题
-
9. 如图，E、B、F、C在同一条直线上，若∠D＝∠A＝90°，EB＝FC，AB＝DF．则ΔABC≌ ， 全等的根据是 ．
10. 如图，△ABC中，∠ACB=90°，∠A=30°，CD⊥AB于D，AB=4cm，则∠BCD= ， BD= ．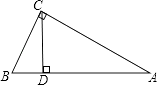
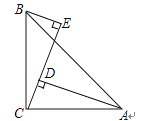
11. 判定两直角三角形全等的各种条件：（1）一锐角和一边对应相等（2）两边对应相等（3）两锐角对应相等．其中能得到两个直角三角形全等的条件是12.如图，∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D，下面四个结论：
①∠ABE=∠BAD；②△CEB≌△ADC；
③AB=CE；④AD﹣BE=DE．
正确的是 （将你认为正确的答案序号都写上）．
13. 如图，在Rt△ABC与Rt△DCB中，已知∠A=∠D=90°，请你添加一个条件（不添加字母和辅助线），使Rt△ABC≌Rt△DCB，你添加的条件是 ．
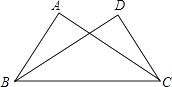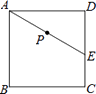
14.如图，E为正方形ABCD中CD边上一点，∠DAE=30°，P为AE的中点，过点P作直线分别与AD、BC相交于点M、N．若MN=AE，则∠AMN等于
三、解答题
