人教版数学九年级下册 第二十七章 相似 单元测试题
试卷更新日期：2021-01-08 类型：单元试卷
一、单选题
-
1. 下列说法正确的是（ ）A、所有的等边三角形都相似 B、所有的菱形都相似 C、所有的等腰三角形都相似 D、所有的矩形都相似2. 手工制作课上，小红利用一些花布的边角料，剪裁后装饰手工画，下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边，其中，每个图案花边的宽度都相等，那么，每个图案中花边的内外边缘所围成的几何图形不一定相似的是（ ）A、
B、
C、
D、
3. 在下列四组线段中，成比例线段的是（ ）A、3、4 、5 、6 B、4 、8、3、5 C、5、15 、2 、6 D、8 、4 、1、354. 如图所示，下列条件中能单独判断△ABC∽△ACD的个数是（ ）个．①∠ABC＝∠ACD；②∠ADC＝∠ACB；③ ＝ ；④AC2＝AD•AB
A、1 B、2 C、3 D、45. 如图，在△ABC与△ADE中，∠ACB =∠AED =90°，∠ABC=∠ADE ， 连接BD、CE ， 若AC︰BC=3︰4，则BD︰CE为（ ）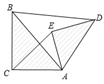
A、5︰3 B、4︰3 C、 ︰2 D、2︰6. 如图，在△ABC中，CD平分∠ACB，过D作BC的平行线交AC于M，若BC=m，AC=n，则DM=（ ）
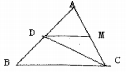A、 B、 C、 D、7. 某校数学兴趣小组为测量学校旗杆AC的高度，在点F处竖立一根长为1.5米的标杆DF ， 如图所示，量出DF的影子EF的长度为1米，再量出旗杆AC的影子BC的长度为6米，那么旗杆AC的高度为（ ）
A、6米 B、7米 C、8.5米 D、9米8. 如图，身高为1.6 m的某学生想测量学校旗杆的高度，当他站在C处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得AC＝2 m，BC＝8 m，则旗杆的高度是（ ）
A、6.4m B、7m C、8m D、9m9. 如图2，以点O为位似中心，画一个四边形A'B'C'D'，使它与四边形ABCD位似，且相似比为 ，则下列说法错误的是（ ）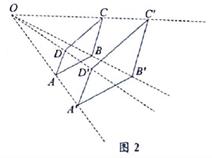
A、四边形ABCD∽四边形A'B'C'D' B、点C，O，C' 三点在同一直线上 C、 D、OB= OB'10.如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，分析下列四个结论：
①△AEF∽△CAB；②CF=2AF；③DF=DC；④tan∠CAD= ．
其中正确的结论有（ ）
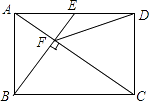A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 在比例尺为1：10000的地图上，一块面积为2平方厘米的区域表示的实际面积为平方米。12. 以小正方形的中心为位似中心，以1：3的比例放大得到一个大正方形，从而得到了一个如图所示的飞镖游戏板.若小明同学向该游戏板投掷飞镖一次（假设飞镖落在游戏板上），则镖落在阴影部分的概率是.
13. 如图，正方形ABCD中，△ABC绕点A逆时针旋转到AB′C′，AB′，AC′分别交对角线BD于点EF，若AE=8，则EF•ED的值为 ．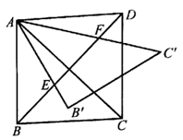
14. 如图，体育兴趣小组选一名身高1.6m的同学直立于旗杆影子的顶端处，其他人分为两部分，一部分同学测得该同学的影长为1.2m，另一部分同学测得同一时刻旗杆影长为9m，那么旗杆的高度是m．
15. 如图，为测量小河两岸A、B两点之间的距离，在小河一侧选出一点C观测A、B两点，并使∠ACB=90º ， 若CD⊥AB ， 垂足为D ， 测得AD=10m ， AC=24m ， 根据所测得的数据可算出A、B之间的距离是m．
16. 如图，在 中， ， 于点 ， 于点 ．交 于点 ，点 在直线 上运动， ， ， ，则 的最小值是 ．
17. 如图，△ABC中，A，B两个顶点在x轴的上方，点C的坐标是（﹣1，0），以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C，并把△ABC的边长放大到原来的2倍．设点B的对应点B′的横坐标是2，则点B的横坐标是 ．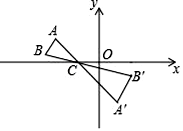
三、解答题
-
18. 如图，在矩形ABCD中，E是AD边上的一点，BE⊥AC，垂足为点F。求证：△AEF∽△CAB.
19. 如图，已知面积为 的锐角 中， ，四边形DEFG是 的内接正方形（四边形的各顶点在三角形的边上），求：正方形DEFG的边长．
20. 某天，小芳走到如图所示的C处时，看到正对面一条东西走向的笔直公路.上有一辆汽车从东面驶来，到达Q处时，恰好被公路北侧边上竖着的一个长12m的广告牌AB挡住，3s后在P处又重新看到该汽车的全部车身，已知该汽车的行驶速度是6m/s，假设AB PQ，公路宽为10m，求小芳所在C处到公路南侧PQ的距离.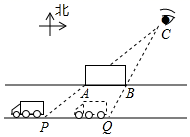
四、作图题
-
21. 已知△ABC在平面直角坐标系内，三个顶点的坐标分别为A(0，3)，B(4，5)，C(3，2)．(正方形网格中，每个小正方形的边长都是1个单位长度)
(1)、画出△ABC向下平移5个单位长度得到的 ，并直接写出点 的坐标；(2)、以点B为位似中心，在网格中画出 ，使 与 位似，且相似比为2∶1，并直接写出 的面积．22. 在平面直角坐标系中， 的三个顶点的坐标分别是 ， ， ．
(1)、画出 关于 轴成轴对称的 ；(2)、画出 以点O为位似中心，位似比为 的 ．并写出 的坐标．五、综合题
-
23. 已知在Rt△ABC中，∠ACB=90 °，AC=4、BC=3，CD⊥AB于D，点M从点D出发，沿线段DC向点C运动，点N从点C出发，沿线段CA向点A运动，两点同时出发，运动速度都是每秒1个单位长度。当点M运动到点C时，两点都停止，设运动时间为t秒。
(1)、如图1，当MN//AB时，求t的值.(2)、如图2，①当t=时，CM=CN；②当MC=MN时，求t的值；
(3)、如图3，是否存在值，使N、M、B三点在同一直线上？若存在，请直接写出t的值；若不存在，请说明理由。24. 如图，抛物线 交x轴于A ， B两点，交y轴于点C ， 直线BC的表达式为y=-x+3．
(1)、求抛物线的表达式；(2)、动点D在直线BC上方的二次函数图象上，连接DC ， DB ， 设△BCD的面积为S ， 求S的最大值；(3)、当点D为抛物线的顶点时，在坐标轴上是否存在一点Q ， 使得以A ， C ， Q为顶点的三角形与△BCD相似？若存在，请求出点Q的坐标；若不存在，请说明理由．