浙江省浙南名校联盟2020-2021学年高一上学期数学期中考试试卷
试卷更新日期:2021-01-08 类型:期中考试
一、单选题
-
1. 设 , , ,则 ( )A、 B、 C、 D、2. 已知函数 ,则函数 的定义域为( )A、 B、 C、 D、3. 设 ,则“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件4. 若 ,则( )A、 B、 C、 D、5. 下列函数既是偶函数,又在 上单调递减的函数是( )A、 B、 C、 D、6. 设 , , ,则 、 、 的大小关系为( )A、 B、 C、 D、7. 函数 的图象大致为( )A、
 B、
B、 C、
C、 D、
D、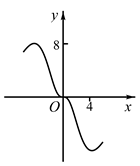 8. 已知函数 , ,若存在 ,使得 ,则实数 的取值范围是( )A、 B、 C、 D、9. 设 , ,则 的最小值为( )A、 B、 C、 D、10. 已知函数 ,当 时,恒有不等式 成立,则实数t的取值范围是( )A、 B、 C、 D、
8. 已知函数 , ,若存在 ,使得 ,则实数 的取值范围是( )A、 B、 C、 D、9. 设 , ,则 的最小值为( )A、 B、 C、 D、10. 已知函数 ,当 时,恒有不等式 成立,则实数t的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 已知幂函数 在 上为增函数,则 .12. 计算: .13. 函数 的值域为 .14. 已知命题p: ,使得 .若 是真命题,则实数a的取值范围为 .15. 若a,b为实数,且 ,则 的最小值是 .16. 若有限集合 ,定义集合 中的元素个数为集合A的“容量”,记为 ,现已知 ,且 ,则正整数m的值是 .
三、解答题
-
17. 设集合 ,集合 .(1)、当 时,求 ;(2)、若 ,求实数m的取值范围.18. 已知函数 , .(1)、当 时,求 的最小值;(2)、设 的最小值为 ,求 的表达式.