吉林省白城市通榆县2020-2021学年九年级上学期数学第四次月考试卷
试卷更新日期：2021-01-08 类型：月考试卷
一、单项选择题(每小题2分，共12分)
-
1. 下列图形中，是中心对称图形但不是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列事件中，是必然事件的是（ ）A、从一个只有红球的盒子里摸出一个球是红球 B、买一张电影票，座位号是5的倍数 C、掷一枚质地均匀的硬币，正面向上 D、走过一个红绿灯路口时，前方正好是红灯3. 方程5x2=4x的解是（ ）A、x=0 B、x= C、x1=0，x2= D、x1=0，x2=4. 如图，a<0，b>0，c<0，那么二次函数y=ax2+bx+c的图像可能是（ ）A、
B、
C、
D、
5. 如图，在Rt△ABC中，∠ACB=90°，∠BAC=33°，把△ABC绕点A按顺时针方向旋转∠BAC的大小，得到△AB'C'， 延长BC交B'C'于点D，则∠BDC'等于（ ）
A、143° B、147° C、157° D、153°6. 如图，AB是⊙O的直径，直线PA与⊙O相切于点A，PO交⊙O于点C，连接BC，若∠BCO=a，则∠P的度数为（ ）
A、2a B、90°-2a C、45°-2a D、45°+2a二、填空题(每小题3分，共24分)
-
7. 在平而直角坐标系中，点(-3，4)关于原点对称的点的坐标是。8. 将方程x2+6x-3=0化为(x+h)2=k的形式是。9. 以m=为反例，可以证明“关于x的一元二次方程x2+x+m=0必有实数根”是错误的命题(写出一个m的值即可)。10. 为解决民生问题，国家对某药品价格分两次降价，该药品的原价是48元，降价后的价格是30元，若平均每次降价的百分率均为x，可列方程为 。11. 如图，点A是反比例函数y= 图像上一点，过点A作AB⊥y轴于点B，点C，D在x轴上，且BC∥AD，四边形ABCD的面积为4，则k= 。
12. 如图，正六边形ABCDEF内接于⊙O，若AB=2，则⊙O的半径为。
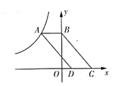
13. 如图，扇形的圆心角为90°，半径OC=4，∠AOC=30°，CD⊥OB于点D，则阴影部分的面积是。
14. 如图，在平面直角坐标系中，过点P(m，0)作x轴的垂线，分别交抛物线y=x2+ x+2和直线y= x-2于点A和点C，以线段AC为对角线作正方形ABCD，则当正方形ABCD的面积最小时m的值为。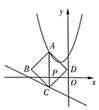
三、解答题(每小题5分，共20分)
-
15. 解方程：3x2-x-1=016. 如图，△ABC为等边三角形，将AC边绕点C顺时针旋转40°，得到线段CD，连接BD，求∠ABD的度数。
17. 如图，三张“黑桃”扑克牌，背面完全相同，现将三张扑克牌背面朝上，洗勾后放在桌面上，甲、乙两人进行摸牌游戏，甲先从中随机抽取一张，记下数字后再放回洗匀，乙再从中随机抽取一张。
(1)、“甲抽到‘黑桃”这一事件是事件(填“不可能“随机"或“必然”)；(2)、利用画树状图或列表的方法，求甲、乙两人抽到同一张扑克牌的概率。18. 在压力不变的情况下，某物体所受的压强p(Pa)与它的受力面积S(m2)之间成反比例关系，其图像如图所示。
(1)、求p与s之间的函数关系式；(2)、当s=0.4m2时，求该物体所受的压强p。四、解答题(每小题7分，共28分)
-
19.
(1)、图|是4×4的正方形网格，请在其中选取一个白色的正方形并涂上阴影，使阴影部分是一个中心对你图形；(2)、如图2，在正方形网格中，以点A为旋转中心，将△ABC按逆时针方向旋转90°，画出旋转后的△AB1C1；(3)、如图3，在边长为1个单位长度的小正方形组成的网格中，点A，B，C，O都是格点，作△ABC关于点O的中心对称图形△AB1C120. 如图，二次函数y=ax2+bx的图像经过点A(2，4)与B(6，0)。
(1)、求a，b的值；(2)、若点C是该二次函数的最高点，求△OBC的面积。21. 如图，在△ABC中，∠C=90°，点O在边AB上，以O为圆心、OA为半径作圆，⊙O与边AC的另一个交点为D，BD恰好为⊙O的切线。
(1)、求证：∠A=∠CBD；(2)、若∠CBD=36°，⊙O的半径为2，求 的长(结果保留π)。22. 一段长为30m的墙前有一块矩形空地ABCD，用篱笆围成如图所示的图形，共用去100 m(靠墙的一边不用围，篱笆的厚度忽略不计)，其中四边形AEFH和四边形CDHG是矩形，四边形EBGF是边长为10m的正方形，设CD=xm。
(1)、填空：CG=m(用含x的代数式表示)；(2)、若矩形CDHG的面积为125m2 ， 求CD的长；(3)、当CD的长为多少米时，矩形ABCD的面积最大？五、解答题(每小题8分，共16分)
-
23. 如图，平行于y轴的直尺(部分)与反比例函数y= (x>0)的图像交于A，C两点，与x轴交于B，D两点，连接AC，点A、B对应直尺上的刻度分别为5，2。直尺的宽度
BD=2，OB=2．设直线AC的解析式为y=kx+b。
(1)、请结合图像直接写出：①点A的坐标是；
②不等式kx+b> (x>0)的解集是。
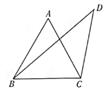
(2)、求直线AC的解析。24. 已知：如图1，△ABC中，AB=AC，∠BAC=60°，D，E分别是AB，AC上的点，AD=AE，不难发现BD与CE的数量关系。
(1)、将△ADE绕点A旋转到图2位置时，直接写出BD与CE的数量关系；(2)、当∠BAC=90°时，将OADE绕点A旋转到图3位置(其他条件不变)．①猜想BD与CE有什么位置和数量关系，并就图3的情形进行证明；
②在△ADE绕点A旋转的过程中，当点C，D，E在同一直线上时，直接写出∠ADB的度数。
六、解答题(每小题10分，共20分)
-
25. 如图，在平面直角坐标系中，线段AB的端点为A(1，1)，B(3，1)，当函数y= (x>0)的图像与线段AB有交点时，设交点为P(点P不与点A，B重合)。
(1)、直接写出k的取值范围；(2)、将线及PB绕点P逆时针旋转90°得列线段PQ，以PA，PQ为边作矩形APQM．①若函数y= (x>0)的图像恰好经过点M，求k的值；
②若函数y= (x>0)的图像与矩形APQM的边AM有公共点，则k的值不可能
为（ ）
A．
B.2
C．
D．
③设矩形APQM的边与函数y= (x>0)的图像的交点为N(除点P)，并连接PN，当PN将矩形APQM的面积分成1：3两部分时，直接写出点P的横坐标。
26. 如图，在平而直角坐标系中，经过原点的抛物线y=-x2+4mx(m>0)与x轴的另一个个点为A，过点P(1，m)作直线PB⊥x轴，交抛物线于点B，作点B关于抛物线对称轴的对称点C(点B，C不重合)，连接BC，当点P，B不重合时，以BP，BC为边，作矩形PBCQ，设矩形PBCQ的周长为1。
(1)、当m=1时，点A的坐标为；(2)、当BC= 时，求这条抛物线所对应的函数解析式；(3)、当点P在点B下方时，求l与m之间的函数关系式；(4)、连接CP，以CP为直角边作等腰直角三角形PCM，当点M落在x轴上时，直接写出m的值。