湖南省株洲市醴陵市2019-2020学年九年级下学期数学开学考试试卷
试卷更新日期:2021-01-08 类型:开学考试
一、单选题
-
1. 8的相反数是( )A、8 B、 C、 D、2. 单项式9xmy3与单项式4x2yn是同类项,则m+n的值是( )A、2 B、5 C、4 D、33. 世卫组织数据显示,截至北京时间3月29日16时,全球新冠肺炎确诊病例超过630000例,将630000用科学记数法表示是( )A、 B、 C、 D、4. 用配方法解方程 ,下列配方正确的是( )A、 B、 C、 D、5. 如图,直线 交于点O,射线 平分 ,若 ,则 等于( )
 A、 B、 C、 D、6. 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A、 B、 C、 D、6. 如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )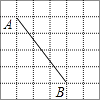 A、5 B、6 C、7 D、257. 如图,矩形 的对角线 ,则 的长为( )
A、5 B、6 C、7 D、257. 如图,矩形 的对角线 ,则 的长为( ) A、 B、 C、 D、8. 如图,在 中, ,则 四边形 =( )
A、 B、 C、 D、8. 如图,在 中, ,则 四边形 =( ) A、7 B、8 C、9 D、109. 在 中, ,则 的值为( )A、 B、 C、 D、10. 如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )
A、7 B、8 C、9 D、109. 在 中, ,则 的值为( )A、 B、 C、 D、10. 如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( ) A、 B、 C、3 D、4
A、 B、 C、3 D、4二、填空题
-
11. 计算:= .
12. 因式分解:13. 分式方程 的解是14. 不等式组 的解集是 ,则m的取值范围是15. 等腰三角形的一条边长为7,另一边长为15,则它的周长为16. 在菱形 中,若对角线长 ,则边长 .17. 某班五个合作学习小组人数如下:5、5、 、6、7,已知这组数据的平均数是6,则这组数据的中位数是18. 如图,在等边△ABC中,AB=4,点P是BC边上的动点,点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是.
三、解答题
-
19.20. 先化简,再求值: ,其中 .21. 今年4月,国民体质监测中心等机构开展了青少年形体测评.专家组随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问:
 (1)、在这次形体测评中,一共抽查了名学生;(2)、请将条形统计图补充完整;(3)、如果全市有1万名初中生,那么全市初中生中,坐姿不良的学生约有人.22. 如图, 是 的角平分线,点 分别在 上,且 .
(1)、在这次形体测评中,一共抽查了名学生;(2)、请将条形统计图补充完整;(3)、如果全市有1万名初中生,那么全市初中生中,坐姿不良的学生约有人.22. 如图, 是 的角平分线,点 分别在 上,且 . (1)、求证: ;(2)、若 ,求四边形 的面积.23. 如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
(1)、求证: ;(2)、若 ,求四边形 的面积.23. 如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内. (1)、求居民楼AB的高度;(2)、求C、A之间的距离.(结果保留根号)24. 对于实数 ,若存在坐标 同时满足一次函数 和反比例函数 ,则二次函数 为一次函数和反比例函数的“共享”函数.(1)、试判断(需要写出判断过程):一次函数 和反比例函数 是否存在“共享”函数?若存在,写出它们的“共享”函数和实数对坐标;(2)、已知整数 满足条件: ,并且一次函数 与反比例函数 存在“共享”函数 ,求整数m的值.25. 如图,已知抛物线 与 轴交于 ,且点 ,与y轴交于点 ,其对称轴为直线 .
(1)、求居民楼AB的高度;(2)、求C、A之间的距离.(结果保留根号)24. 对于实数 ,若存在坐标 同时满足一次函数 和反比例函数 ,则二次函数 为一次函数和反比例函数的“共享”函数.(1)、试判断(需要写出判断过程):一次函数 和反比例函数 是否存在“共享”函数?若存在,写出它们的“共享”函数和实数对坐标;(2)、已知整数 满足条件: ,并且一次函数 与反比例函数 存在“共享”函数 ,求整数m的值.25. 如图,已知抛物线 与 轴交于 ,且点 ,与y轴交于点 ,其对称轴为直线 . (1)、求这条抛物线的解析式;(2)、若在x轴上方的抛物线上有点D,使 的内心恰好在x轴上,求此时 的面积;(3)、在直线 上方的抛物线上有一动点P,过P作 轴,垂足为M是否存在P点,使得以 为顶点的三角形与 相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
(1)、求这条抛物线的解析式;(2)、若在x轴上方的抛物线上有点D,使 的内心恰好在x轴上,求此时 的面积;(3)、在直线 上方的抛物线上有一动点P,过P作 轴,垂足为M是否存在P点,使得以 为顶点的三角形与 相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.