湖南省长沙市长郡双语2019-2020学年九年级下学期数学开学考试试卷
试卷更新日期:2021-01-08 类型:开学考试
一、单选题
-
1. −4的绝对值是( )A、4 B、−4 C、 D、2. 据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338 600 000亿次,数字338 600 000用科学记数法可简洁表示为( )A、3.386×108 B、0.3386×109 C、33.86×107 D、3.386×1093. 下列手机软件图标中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 点 在y轴上,则点M的坐标为( )A、 B、 C、 D、5. 下列说法正确的是( )A、“打开电视剧,正在播足球赛”是必然事件 B、甲组数据的方差S甲2=0.24,乙组数据的方差S乙2=0.03,则乙组数据比甲组数据稳定 C、一组数据2,4,5,5,3,6的众数和中位数都是5 D、“掷一枚硬币正面朝上的概率是”表示每抛硬币2次就有1次正面朝上6. 如图是一个正方体纸盒的外表面展开图,则这个正方体是( )
4. 点 在y轴上,则点M的坐标为( )A、 B、 C、 D、5. 下列说法正确的是( )A、“打开电视剧,正在播足球赛”是必然事件 B、甲组数据的方差S甲2=0.24,乙组数据的方差S乙2=0.03,则乙组数据比甲组数据稳定 C、一组数据2,4,5,5,3,6的众数和中位数都是5 D、“掷一枚硬币正面朝上的概率是”表示每抛硬币2次就有1次正面朝上6. 如图是一个正方体纸盒的外表面展开图,则这个正方体是( )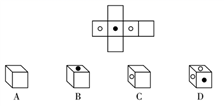 A、A B、B C、C D、D7.
A、A B、B C、C D、D7.如图,在菱形ABCD中,AB=5,∠BCD=120°,则△ABC的周长等于( )
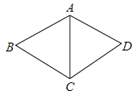 A、20 B、15 C、10 D、58. 如图,P为⊙O外一点,PA切⊙O于点A,⊙O的半径为6,且PA=8,则cos∠APO等于( )
A、20 B、15 C、10 D、58. 如图,P为⊙O外一点,PA切⊙O于点A,⊙O的半径为6,且PA=8,则cos∠APO等于( )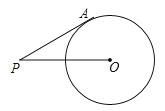 A、 B、 C、 D、9. 一元二次方程x2+kx﹣3=0的一个根是x=1,则另一个根是( )A、3 B、﹣1 C、﹣3 D、﹣210. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的大致图象为( )
A、 B、 C、 D、9. 一元二次方程x2+kx﹣3=0的一个根是x=1,则另一个根是( )A、3 B、﹣1 C、﹣3 D、﹣210. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的大致图象为( )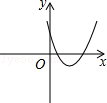 A、
A、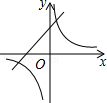 B、
B、 C、
C、 D、
D、 11. 如图,∠ACB=90°,CD是AB边上的高,若AD=24,BD=6,则CD的长是( )
11. 如图,∠ACB=90°,CD是AB边上的高,若AD=24,BD=6,则CD的长是( )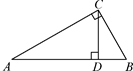 A、8 B、10 C、12 D、1412. 如图,在平面直角坐标系中,点B在第一象限, 轴于点A,反比例函数 ( )的图象与线段 相交于点C,且C是线段 的中点,点C关于直线 的对称点 的坐标为 ,若 的面积为3,则k的值为( )
A、8 B、10 C、12 D、1412. 如图,在平面直角坐标系中,点B在第一象限, 轴于点A,反比例函数 ( )的图象与线段 相交于点C,且C是线段 的中点,点C关于直线 的对称点 的坐标为 ,若 的面积为3,则k的值为( ) A、 B、1 C、2 D、3
A、 B、1 C、2 D、3二、填空题
-
13. 若式子有意义,则x的取值范围是14. 分解因式: .15. 已知圆锥的底面半径为 ,母线长为 ,则圆锥的侧面积是.16. 如图,四边形ABCD中,AB∥CD , 要使四边形ABCD为平行四边形,则可添加的条件为.(填一个即可)
 17. 三角形的中位线把三角形分成的两部分的面积之比是 .
17. 三角形的中位线把三角形分成的两部分的面积之比是 .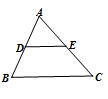 18. 如图,抛物线 的图象与坐标轴交于点A , B , D , 顶点为E , 以AB为直径画半圆交y正半轴交于点C , 圆心为M , P是半圆上的一动点,连接EP . ①点E在⊙M的内部;②CD的长为 ;③若P与C重合,则∠DPE=15°;④在P的运动过程中,若AP= ,则PE= ⑤N是PE的中点,当P沿半圆从点A运动至点B时,点N运动的路径长是2π.其中结论正确的是
18. 如图,抛物线 的图象与坐标轴交于点A , B , D , 顶点为E , 以AB为直径画半圆交y正半轴交于点C , 圆心为M , P是半圆上的一动点,连接EP . ①点E在⊙M的内部;②CD的长为 ;③若P与C重合,则∠DPE=15°;④在P的运动过程中,若AP= ,则PE= ⑤N是PE的中点,当P沿半圆从点A运动至点B时,点N运动的路径长是2π.其中结论正确的是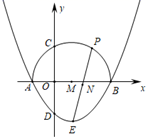
三、解答题
-
19. 计算:( )﹣1﹣2cos30°+ +(3﹣π)020. 先化简,再求值: ,其中x请从不等式组 的解集中选取一个合适的值代入.21. 某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的
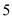 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题: 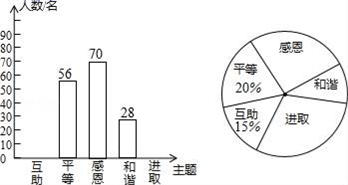 (1)、这次调查的学生共有多少名;(2)、请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数;(3)、如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).22. 已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E .
(1)、这次调查的学生共有多少名;(2)、请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数;(3)、如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).22. 已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E .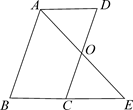 (1)、求证:△AOD≌△EOC;(2)、连接AC、DE , 当∠B=∠AEB=45°时,求证四边形 ACED是正方形.23. 为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)、求证:△AOD≌△EOC;(2)、连接AC、DE , 当∠B=∠AEB=45°时,求证四边形 ACED是正方形.23. 为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)、求w与x之间的函数关系式.(2)、该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?(3)、如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?24. 如图,AD是⊙O的切线,切点为A , AB是⊙O的弦,过点B作BC∥AD , 交⊙O于点C , 连接AC , 过点C作CD∥AB , 交AD于点D , 连接AO并延长交BC于点M , 交过点C的直线于点P , 且∠BCP=∠ACD .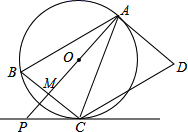 (1)、求证:∠BAP=∠CAP;(2)、判断直线PC与⊙O的位置关系,并说明理由;(3)、若AB=5 ,BC=10,求PC的长.25. 如图,抛物线y=ax2﹣2ax+c的图象经过点C(0,﹣2),顶点D的坐标为(1,﹣ ),与x轴交于A、B两点.
(1)、求证:∠BAP=∠CAP;(2)、判断直线PC与⊙O的位置关系,并说明理由;(3)、若AB=5 ,BC=10,求PC的长.25. 如图,抛物线y=ax2﹣2ax+c的图象经过点C(0,﹣2),顶点D的坐标为(1,﹣ ),与x轴交于A、B两点.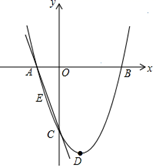 (1)、求抛物线的解析式.(2)、连接AC , E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和 的值.(3)、点C关于x轴的对称点为H,当 FC+BF取最小值时,在抛物线的对称轴上是否存在点Q , 使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.26. 若凸四边形的两条对角线所夹锐角为60°,我们称这样的凸四边形为“美丽四边形”.
(1)、求抛物线的解析式.(2)、连接AC , E为直线AC上一点,当△AOC∽△AEB时,求点E的坐标和 的值.(3)、点C关于x轴的对称点为H,当 FC+BF取最小值时,在抛物线的对称轴上是否存在点Q , 使△QHF是直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.26. 若凸四边形的两条对角线所夹锐角为60°,我们称这样的凸四边形为“美丽四边形”.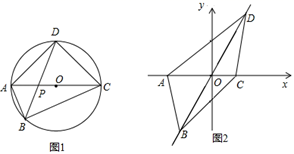 (1)、若矩形ABCD是“美丽四边形”,且AB=3,则BC=;(2)、如图1,“美丽四边形”ABCD内接于⊙O , AC与BD相交于点P , 且对角线AC为直径,AP=1,PC=5,求另一条对角线BD的长;(3)、如图2,平面直角坐标系中,已知“美丽四边形”ABCD的四个顶点A(﹣3,0)、C(2,0),B在第三象限,D在第一象限,AC与BD交于点O , 且四边形ABCD的面积为 ,若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.
(1)、若矩形ABCD是“美丽四边形”,且AB=3,则BC=;(2)、如图1,“美丽四边形”ABCD内接于⊙O , AC与BD相交于点P , 且对角线AC为直径,AP=1,PC=5,求另一条对角线BD的长;(3)、如图2,平面直角坐标系中,已知“美丽四边形”ABCD的四个顶点A(﹣3,0)、C(2,0),B在第三象限,D在第一象限,AC与BD交于点O , 且四边形ABCD的面积为 ,若二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.