2016年山东省临沂市中考数学试卷
试卷更新日期:2016-07-05 类型:中考真卷
一、(共14小题,每小题3分,满分42分)在每小题给出的四个选项中,只有一个是符合题目要求的.
-
1. 四个数﹣3,0,1,2,其中负数是( )A、﹣3 B、0 C、1 D、22.
如图,直线AB∥CD,∠A=40°,∠D=45°,则∠1的度数是( )
 A、80° B、85° C、90° D、95°3. 下列计算正确的是( )A、x3﹣x2=x B、x3•x2=x6 C、x3÷x2=x D、(x3)2=x54. 不等式组 的解集,在数轴上表示正确的是( )A、
A、80° B、85° C、90° D、95°3. 下列计算正确的是( )A、x3﹣x2=x B、x3•x2=x6 C、x3÷x2=x D、(x3)2=x54. 不等式组 的解集,在数轴上表示正确的是( )A、 B、
B、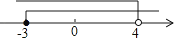 C、
C、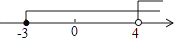 D、
D、 5.
5.如图,一个空心圆柱体,其主视图正确的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 6. 某校九年级共有1、2、3、4四个班,现从这四个班中随机抽取两个班进行一场篮球比赛,则恰好抽到1班和2班的概率是( )A、 B、 C、 D、7. 一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )A、108° B、90° C、72° D、60°8. 为了绿化校园,30名学生共种78棵树苗.其中男生每人种3棵,女生每人种2棵,该班男生有x人,女生有y人.根据题意,所列方程组正确的是( )A、 B、 C、 D、9.
6. 某校九年级共有1、2、3、4四个班,现从这四个班中随机抽取两个班进行一场篮球比赛,则恰好抽到1班和2班的概率是( )A、 B、 C、 D、7. 一个正多边形的内角和为540°,则这个正多边形的每一个外角等于( )A、108° B、90° C、72° D、60°8. 为了绿化校园,30名学生共种78棵树苗.其中男生每人种3棵,女生每人种2棵,该班男生有x人,女生有y人.根据题意,所列方程组正确的是( )A、 B、 C、 D、9.某老师为了解学生周末学习时间的情况,在所任班级中随机调查了10名学生,绘成如图所示的条形统计图,则这10名学生周末学习的平均时间是( )
 A、4 B、3 C、2 D、110.
A、4 B、3 C、2 D、110.如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D,C.若∠ACB=30°,AB= ,则阴影部分的面积是( )
 A、 B、 C、﹣ D、﹣11.
A、 B、 C、﹣ D、﹣11.用大小相等的小正方形按一定规律拼成下列图形,则第n个图形中小正方形的个数是( )
 A、2n+1 B、n2﹣1 C、n2+2n D、5n﹣212.
A、2n+1 B、n2﹣1 C、n2+2n D、5n﹣212.如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
 A、0 B、1 C、2 D、313. 二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
A、0 B、1 C、2 D、313. 二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:x
…
﹣5
﹣4
﹣3
﹣2
﹣1
0
…
y
…
4
0
﹣2
﹣2
0
4
…
下列说法正确的是( )
A、抛物线的开口向下 B、当x>﹣3时,y随x的增大而增大 C、二次函数的最小值是﹣2 D、抛物线的对称轴是x=﹣14.如图,直线y=﹣x+5与双曲线y= (x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是 .若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线y= (x>0)的交点有( )
 A、0个 B、1个 C、2个 D、0个,或1个,或2个
A、0个 B、1个 C、2个 D、0个,或1个,或2个二、填空题(共5小题,每小题3分,满分15分)
-
15. 分解因式:x3﹣2x2+x= .
16. 化简 = .17.如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB.若AB=8,BD=3,BF=4,则FC的长为 .
 18.
18.如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB=4,BC=8,则△ABF的面积为 .
 19. 一般地,当α、β为任意角时,sin(α+β)与sin(α﹣β)的值可以用下面的公式求得:sin(α+β)=sinα•cosβ+cosα•sinβ;sin(α﹣β)=sinα•cosβ﹣cosα•sinβ.例如sin90°=sin(60°+30°)=sin60°•cos30°+cos60°•sin30°= × + × =1.类似地,可以求得sin15°的值是 .
19. 一般地,当α、β为任意角时,sin(α+β)与sin(α﹣β)的值可以用下面的公式求得:sin(α+β)=sinα•cosβ+cosα•sinβ;sin(α﹣β)=sinα•cosβ﹣cosα•sinβ.例如sin90°=sin(60°+30°)=sin60°•cos30°+cos60°•sin30°= × + × =1.类似地,可以求得sin15°的值是 .
三、解答题(共7小题,满分63分)
-
20. 计算:|﹣3|+ tan30°﹣ ﹣(2016﹣π)0 .21.
为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
身高分组
频数
百分比
x<155
5
10%
155≤x<160
a
20%
160≤x<165
15
30%
165≤x<170
14
b
x≥170
6
12%
总计
100%
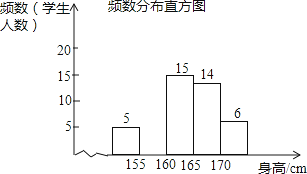 (1)、填空:a= , b=;
(1)、填空:a= , b=;
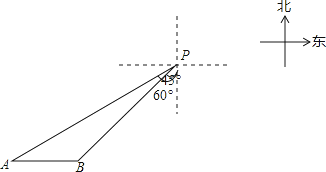
(2)、补全频数分布直方图;(3)、该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?22.一艘轮船位于灯塔P南偏西60°方向,距离灯塔20海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据: ≈1.732,结果精确到0.1)?
 23.
23.如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.
 (1)、求证:△ABC是等边三角形;(2)、若∠PAC=90°,AB=2 ,求PD的长.24. 现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.(1)、请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;(2)、小明选择哪家快递公司更省钱?25.
(1)、求证:△ABC是等边三角形;(2)、若∠PAC=90°,AB=2 ,求PD的长.24. 现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.(1)、请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;(2)、小明选择哪家快递公司更省钱?25.如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
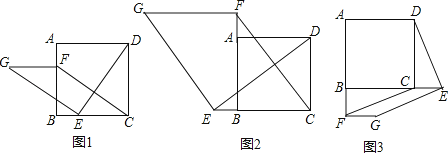 (1)、请判断:FG与CE的数量关系是 , 位置关系是;(2)、如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;(3)、如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.26.
(1)、请判断:FG与CE的数量关系是 , 位置关系是;(2)、如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;(3)、如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.26.如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.
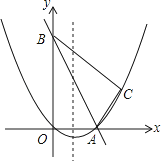 (1)、求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;(2)、动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?(3)、在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
(1)、求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;(2)、动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?(3)、在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.