河北省青县22019-2020学年九年级下学期数学开学考试试卷
试卷更新日期:2021-01-08 类型:开学考试
一、单选题
-
1. 若一个角为65°,则它的补角的度数为( )
A、25° B、35° C、115° D、125°2. 下列各式,不能表示y是x的函数的是( )A、 B、 C、 D、3. 在下列图形中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 给出下列命题:
4. 给出下列命题:①三条线段组成的图形叫三角形;②三角形相邻两边组成的角叫三角形的内角;
③三角形的角平分线是射线;
④三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外;
⑤任何一个三角形都有三条高、三条中线、三条角平分线;
⑥三角形的三条角平分线交于一点,且这点在三角形内.
正确的命题有( )
A、1个 B、2个 C、3个 D、4个5. 如图,直线a,b,c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )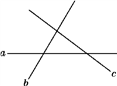 A、一处 B、两处 C、三处 D、四处6. 如果 ,那么x的值为( )A、2或-1 B、0或1 C、2 D、-17. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
A、一处 B、两处 C、三处 D、四处6. 如果 ,那么x的值为( )A、2或-1 B、0或1 C、2 D、-17. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( ) A、①,② B、①,④ C、③,④ D、②,③8. 关于x的不等式 的解集为x>3,那么a的取值范围为( )A、a>3 B、a<3 C、a≥3 D、a≤39. 如图, , , , ,垂足分别是点D,E, , .则 的面积是( )
A、①,② B、①,④ C、③,④ D、②,③8. 关于x的不等式 的解集为x>3,那么a的取值范围为( )A、a>3 B、a<3 C、a≥3 D、a≤39. 如图, , , , ,垂足分别是点D,E, , .则 的面积是( )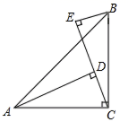 A、 B、5 C、 D、10. 如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )
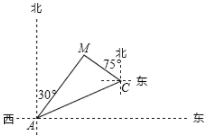
A、 B、5 C、 D、10. 如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )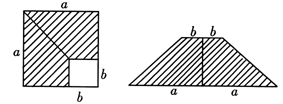 A、 B、 C、 D、无法确定11. 如图,某天然气公司的主输气管道从A市的北偏东 方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东 方向,测绘员由A处沿主输气管道步行1000米到达点C处,测得M小区位于点C的北偏西 方向,试在主输气管道上寻找支管道连接点N,使点N到该小区铺设的管道最短,此时铺设的管道的最短距离约是( ).
A、 B、 C、 D、无法确定11. 如图,某天然气公司的主输气管道从A市的北偏东 方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东 方向,测绘员由A处沿主输气管道步行1000米到达点C处,测得M小区位于点C的北偏西 方向,试在主输气管道上寻找支管道连接点N,使点N到该小区铺设的管道最短,此时铺设的管道的最短距离约是( ).(参考数据: , )
 A、366米 B、650米 C、634米 D、700米12. 在矩形 中,点E在 上, , ,垂足为F,且 , ,则 的值是( )
A、366米 B、650米 C、634米 D、700米12. 在矩形 中,点E在 上, , ,垂足为F,且 , ,则 的值是( )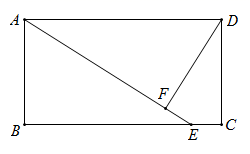 A、2 B、 C、 D、13. 如图,正比例函数y=x与反比例y= 的图象相交于A、C两点,AB⊥x轴于B,CD⊥x轴于D,则四边形ABCD的面积为( )
A、2 B、 C、 D、13. 如图,正比例函数y=x与反比例y= 的图象相交于A、C两点,AB⊥x轴于B,CD⊥x轴于D,则四边形ABCD的面积为( )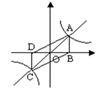 A、1 B、 C、2 D、14. 已知二次函数 的图象经过点 ,则 有( )A、最大值1 B、最大值2 C、最小值0 D、最大值15. 如图,在四边形 中, , , ,E是 的中点.点P以每秒1个单位长度的速度从点A出发,沿 向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿 向点B运动.点P停止运动时,点Q也随之停止运动.若以点 为顶点的四边形是平行四边形,则点P运动的时间为( )
A、1 B、 C、2 D、14. 已知二次函数 的图象经过点 ,则 有( )A、最大值1 B、最大值2 C、最小值0 D、最大值15. 如图,在四边形 中, , , ,E是 的中点.点P以每秒1个单位长度的速度从点A出发,沿 向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿 向点B运动.点P停止运动时,点Q也随之停止运动.若以点 为顶点的四边形是平行四边形,则点P运动的时间为( )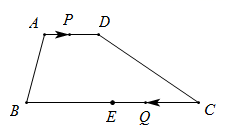 A、1 B、 C、2或 D、1或
A、1 B、 C、2或 D、1或二、填空题
-
16. 下图为张亮的答卷,他的得分应是
姓名:张亮 得分?
填空(每小题20分,共100分)
① 的绝对值是1;
② 的倒数是 ;
③0.5的相反数是 ;
④ 的立方根是2;
⑤ ,0,8的平均数是2
17. 如图,边长为1的正方形网格中,AB3.(填“>”,“=”或“<”) 18. 若 ,则 = .19. 已知:如图,在平面直角坐标系xOy中,点A在抛物线y=x2﹣4x+6上运动,过点A作AC⊥x轴于点C , 以AC为对角线作正方形ABCD , 则抛物线y=x2﹣4x+6的顶点是 , 正方形的边长AB的最小值是 .
18. 若 ,则 = .19. 已知:如图,在平面直角坐标系xOy中,点A在抛物线y=x2﹣4x+6上运动,过点A作AC⊥x轴于点C , 以AC为对角线作正方形ABCD , 则抛物线y=x2﹣4x+6的顶点是 , 正方形的边长AB的最小值是 .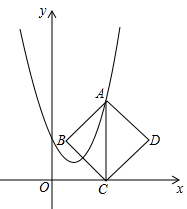
三、解答题
-
20. 嘉嘉准备完成题目:化简: 发现“▲”处被墨水污染了,看不清楚.(1)、琪琪给嘉嘉提供了一个信息:当 时,求值的结果是1,请你帮嘉嘉求出▲代表的是几?(2)、琪琪又给出了正确的化简结果是 .请验证(1)中所求▲是否符合题意.21. 现今“微信运动”被越来越多的人关注和喜爱,石家庄某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整),请根据图中信息,解答下列问题:
步数
频数
频率
8
0.16
15
0.3
12
0.2
3
0.06
c
0.04
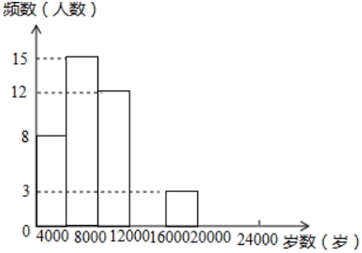 (1)、写出 的值并补全频数分布直方图;(2)、本市约有36200名教师,用调查的样本数据估计日行步数超过12000步(包含12000步)的教师有多少名?(3)、若在50名被调查的教师中,选取日行步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.22. 如图,已知双曲线 经过 斜边的中点D,与直角边 相交于点C,若 的面积为3,求k的值.
(1)、写出 的值并补全频数分布直方图;(2)、本市约有36200名教师,用调查的样本数据估计日行步数超过12000步(包含12000步)的教师有多少名?(3)、若在50名被调查的教师中,选取日行步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.22. 如图,已知双曲线 经过 斜边的中点D,与直角边 相交于点C,若 的面积为3,求k的值.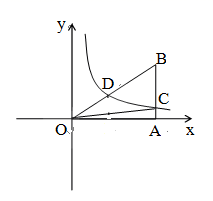 23. 已知:在Rt△ABC中,∠ACB=90°,AC=BC , D是线段AB上一点,连结CD , 将线段CD绕点C逆时针旋转90°得到线段CE , 连结DE , BE .
23. 已知:在Rt△ABC中,∠ACB=90°,AC=BC , D是线段AB上一点,连结CD , 将线段CD绕点C逆时针旋转90°得到线段CE , 连结DE , BE . (1)、依题意补全图形;(2)、若∠ACD=α,用含α的代数式表示∠DEB;(3)、若△ACD的外心在三角形的内部,请直接写出α的取值范围.24. 有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7min同时到达C点,甲机器人前3分钟以a m/min的速度行走,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题:
(1)、依题意补全图形;(2)、若∠ACD=α,用含α的代数式表示∠DEB;(3)、若△ACD的外心在三角形的内部,请直接写出α的取值范围.24. 有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7min同时到达C点,甲机器人前3分钟以a m/min的速度行走,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题: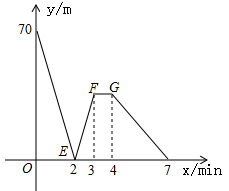 (1)、A、B两点之间的距离是m,A、C两点之间的距离是m,a=m/min;(2)、求线段EF所在直线的函数解析式;(3)、设线段FG∥x轴.
(1)、A、B两点之间的距离是m,A、C两点之间的距离是m,a=m/min;(2)、求线段EF所在直线的函数解析式;(3)、设线段FG∥x轴.①当3≤x≤4时,甲机器人的速度为m/min;
②直接写出两机器人出发多长时间相距28m.
25. 沧州某园林专业户计划投资种植花卉及树木,根据市场调查与预则,种植树木的利润 与投资成本x成正比例关系,种植花卉的利润 与投资成本x的平方成正比例关系,并得到了表格中的数据:投资成本x/万元
2
种植树木的利润 /万元
4
种植花卉的利润 /万元
2
(1)、分别求出利润 与 关于投资成本x的函数解析式;(2)、如果这位专业户计划以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利润W万元,求出W关于m的函数解析式,并求出他至少获得多少利润,他能获取的最大利润是多少?26. 如图,在 中, , , ,以点 为圆心,以 为半径作优弧 ,交 于点 ,交 于点 .点 在优弧 上从点 开始移动,到达点 时停止,连接 .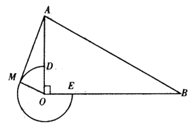

备用图
(1)、当 时,判断 与优弧 的位置关系,并加以证明;(2)、当 时,求点 在优弧 上移动的路线长及线段 的长.(3)、连接 ,设 的面积为 ,直接写出 的取值范围.