2016年江苏省淮安市中考数学试卷
试卷更新日期：2016-07-05 类型：中考真卷
一、选择题
-
1. 下列四个数中最大的数是（ ）A、﹣2 B、﹣1 C、0 D、12. 下列图形是中心对称图形的是（ ）A、
B、
C、
D、
3. 月球的直径约为3476000米，将3476000用科学记数法表示应为（ ）A、0.3476×102 B、34.76×104 C、3.476×106 D、3.476×1084. 在“市长杯”足球比赛中，六支参赛球队进球数如下（单位：个）：3，5，6，2，5，1，这组数据的众数是（ ）A、5 B、6 C、4 D、25. 下列运算正确的是（ ）A、a2•a3=a6 B、（ab）2=a2b2 C、（a2）3=a5 D、a2+a2=a46. 估计 +1的值（ ）
A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间7. 已知a﹣b=2，则代数式2a﹣2b﹣3的值是（ ）
A、1 B、2 C、5 D、78.如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于 MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=4，AB=15，则△ABD的面积是（ ）
A、15 B、30 C、45 D、60二、填空题
-
9. 若分式 在实数范围内有意义，则x的取值范围是 ．10. 分解因式：m2﹣4= ．
11. 点A（3，﹣2）关于x轴对称的点的坐标是 ．
12. 计算：3a﹣（2a﹣b）= ．13. 一个不透明的袋子中装有3个黄球和4个蓝球，这些球除颜色外完全相同，从袋子中随机摸出一个球，摸出的球是黄球的概率是 ．14. 若关于x的一元二次方程x2+6x+k=0有两个相等的实数根，则k= ．15. 若点A（﹣2，3）、B（m，﹣6）都在反比例函数y= （k≠0）的图象上，则m的值是 ．
16. 已知一个等腰三角形的两边长分别为2和4，则该等腰三角形的周长是 ．17. 若一个圆锥的底面半径为2，母线长为6，则该圆锥侧面展开图的圆心角是°．
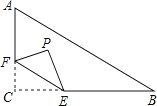
18.如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点F在边AC上，并且CF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是 ．
三、解答题
-
19. 计算：(1)、（ +1）0+|﹣2|﹣3﹣1(2)、解不等式组： ．20. 王师傅检修一条长600米的自来水管道，计划用若干小时完成，在实际检修过程中，每小时检修管道长度是原计划的1.2倍，结果提前2小时完成任务，王师傅原计划每小时检修管道多少米？21.
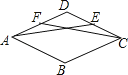
已知：如图，在菱形ABCD中，点E、F分别为边CD、AD的中点，连接AE，CF，求证：△ADE≌△CDF．
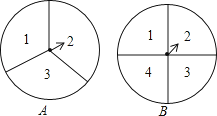
22.如图，转盘A的三个扇形面积相等，分别标有数字1，2，3，转盘B的四个扇形面积相等，分别有数字1，2，3，4．转动A、B转盘各一次，当转盘停止转动时，将指针所落扇形中的两个数字相乘（当指针落在四个扇形的交线上时，重新转动转盘）．
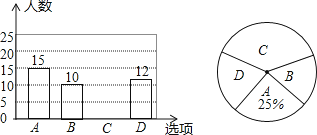
(1)、用树状图或列表法列出所有可能出现的结果；(2)、求两个数字的积为奇数的概率．23.为了丰富同学们的课余生活，某学校举行“亲近大自然”户外活动，现随机抽取了部分学生进行主题为“你最想去的景点是？”的问卷调查，要求学生只能从“A（植物园），B（花卉园），C（湿地公园），D（森林公园）”四个景点中选择一项，根据调查结果，绘制了如下两幅不完整的统计图．
请解答下列问题：
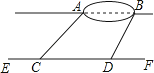
(1)、本次调查的样本容量是；(2)、补全条形统计图；(3)、若该学校共有3600名学生，试估计该校最想去湿地公园的学生人数．24.小宇想测量位于池塘两端的A、B两点的距离．他沿着与直线AB平行的道路EF行走，当行走到点C处，测得∠ACF=45°，再向前行走100米到点D处，测得∠BDF=60°．若直线AB与EF之间的距离为60米，求A、B两点的距离．
25.如图，在Rt△ABC中，∠B=90°，点O在边AB上，以点O为圆心，OA为半径的圆经过点C，过点C作直线MN，使∠BCM=2∠A．
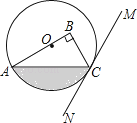(1)、判断直线MN与⊙O的位置关系，并说明理由；(2)、若OA=4，∠BCM=60°，求图中阴影部分的面积．26.甲、乙两家草莓采摘园的草莓品质相同，销售价格也相同．“五一期间”，两家均推出了优惠方案，甲采摘园的优惠方案是：游客进园需购买50元的门票，采摘的草莓六折优惠；乙采摘园的优惠方案是：游客进园不需购买门票，采摘园的草莓超过一定数量后，超过部分打折优惠．优惠期间，设某游客的草莓采摘量为x（千克），在甲采摘园所需总费用为y1（元），在乙采摘园所需总费用为y2（元），图中折线OAB表示y2与x之间的函数关系．
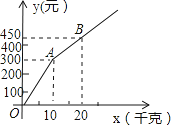(1)、甲、乙两采摘园优惠前的草莓销售价格是每千克元；
(2)、求y1、y2与x的函数表达式；(3)、在图中画出y1与x的函数图象，并写出选择甲采摘园所需总费用较少时，草莓采摘量x的范围．27.如图，在平面直角坐标系中，二次函数y=﹣ x2+bx+c的图象与坐标轴交于A、B、C三点，其中点A的坐标为（0，8），点B的坐标为（﹣4，0）．
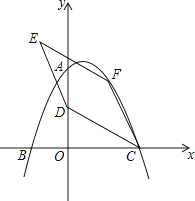(1)、求该二次函数的表达式及点C的坐标；(2)、点D的坐标为（0，4），点F为该二次函数在第一象限内图象上的动点，连接CD、CF，以CD、CF为邻边作平行四边形CDEF，设平行四边形CDEF的面积为S．①求S的最大值；
②在点F的运动过程中，当点E落在该二次函数图象上时，请直接写出此时S的值．
28.问题背景：
如图①，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，探究线段AC，BC，CD之间的数量关系．
小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图②），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE= CD，从而得出结论：AC+BC= CD．
简单应用：
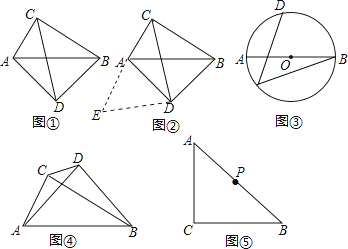(1)、在图①中，若AC= ，BC=2 ，则CD= ．
(2)、如图③，AB是⊙O的直径，点C、D在⊙上， = ，若AB=13，BC=12，求CD的长．拓展规律：
(3)、如图④，∠ACB=∠ADB=90°，AD=BD，若AC=m，BC=n（m＜n），求CD的长（用含m，n的代数式表示）(4)、如图⑤，∠ACB=90°，AC=BC，点P为AB的中点，若点E满足AE= AC，CE=CA，点Q为AE的中点，则线段PQ与AC的数量关系是 ．