上海松江区2020-2021学年九年级上学期数学12月月考试卷
试卷更新日期:2021-01-08 类型:月考试卷
一、单选题
-
1. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )A、 B、 C、 D、2. 函数y=﹣2x2先向右平移1个单位,再向下平移2个单位,所得函数解析式是( )A、y=﹣2(x﹣1)2+2 B、y=﹣2(x﹣1)2﹣2 C、y=﹣2(x+1)2+2 D、y=﹣2(x+1)2﹣23. 已知 和 都是非零向量,在下列选项中,不能判定 的是( )A、 B、 C、 D、4. 一段公路路面的坡度为i=1:2.4.如果某人沿着这段公路向上行走了260m , 那么此人升高了( )A、50m B、100m C、150m D、200m5. 在 中,点 , 分别在边 , 上, ,那么下列条件中能够判断 的是( )A、 B、 C、 D、6. 如图,在平行四边形 中,点E是 边上一点, ,连接 ,且 交于点F.若 ,则 ( )
 A、7 B、15 C、17.5 D、18.5
A、7 B、15 C、17.5 D、18.5二、填空题
-
7. 已知线段a=3cm,b=4cm,那么线段a、b的比例中项等于 cm.
8. 已知点C是线段AB的黄金分割点( ),AB=4,则AC= .9. 已知在△ABC中,∠C=90°,sinA= ,BC=6,则AB的长是 . 10. 已知抛物线 的开口向下,那么k的取值范围是 .11. 二次函数 的图像与 轴的交点坐标是.12. 如果点 和点 是抛物线 上的两点,那么 .(填“>”、“=”、“<”).13. 如图,已知在 中,E是边 的中点, 与对角线 相交于点F.如果 ,那么 (用含 的式子表示).
,BC=6,则AB的长是 . 10. 已知抛物线 的开口向下,那么k的取值范围是 .11. 二次函数 的图像与 轴的交点坐标是.12. 如果点 和点 是抛物线 上的两点,那么 .(填“>”、“=”、“<”).13. 如图,已知在 中,E是边 的中点, 与对角线 相交于点F.如果 ,那么 (用含 的式子表示). 14. 如图,l1//l2//l3 , 直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,若BC=2AB,AD=2,CF=6,则BE的长为 .
14. 如图,l1//l2//l3 , 直线a、b与l1、l2、l3分别交于点A、B、C和点D、E、F,若BC=2AB,AD=2,CF=6,则BE的长为 . 15. 如图,在 中, ,点G是 的重心,如果 ,那么 .
15. 如图,在 中, ,点G是 的重心,如果 ,那么 . 16. 在南海阅兵式上,某架“直-8”型直升飞机在海平面上方1200米的点A处,测得其到海平而观摩点B的俯角为60°,此时点A、B之间的距离是米.17. 如图,一段抛物线: 记为 ,它与x轴交于点 ;将 绕点 旋转 得 ,交x轴于点 ;将 绕点 旋转 得 ,交x轴于点 如此进行下去,则 的顶点坐标是 .
16. 在南海阅兵式上,某架“直-8”型直升飞机在海平面上方1200米的点A处,测得其到海平而观摩点B的俯角为60°,此时点A、B之间的距离是米.17. 如图,一段抛物线: 记为 ,它与x轴交于点 ;将 绕点 旋转 得 ,交x轴于点 ;将 绕点 旋转 得 ,交x轴于点 如此进行下去,则 的顶点坐标是 . 18. 在 中, ,点 分别在边AB、AC上,连接 ,将 沿 翻折,使A落在 上的D处, ,则 .
18. 在 中, ,点 分别在边AB、AC上,连接 ,将 沿 翻折,使A落在 上的D处, ,则 .三、解答题
-
19. 抛物线 上部分点的横坐标x,纵坐标y的对应值如下表:
x
…
-2
-1
0
1
2
…
y
…
0
4
6
6
4
…
求这个二次函数的表达式,并利用配方法求出此抛物线的对称轴、顶点坐标
20. 如图,在 中, 的面积为25,点 分别在边 上, ,已知 . (1)、求 的长.(2)、求四边形 的面积.21. 如图,在 中,AD是BC边上的高, .
(1)、求 的长.(2)、求四边形 的面积.21. 如图,在 中,AD是BC边上的高, .
求:
(1)、线段 的长;(2)、 的值.22. 如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处,一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)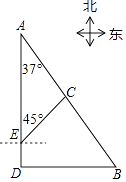 23. 已知:如图,直角梯形 中, ,点E在边 上,点F在对角线 上,且 .
23. 已知:如图,直角梯形 中, ,点E在边 上,点F在对角线 上,且 . (1)、求证: ;(2)、当点E、F分别是边 的中点时,求证: .
(1)、求证: ;(2)、当点E、F分别是边 的中点时,求证: .

