2016年湖南省湘西州中考数学试卷
试卷更新日期：2016-07-05 类型：中考真卷
一、填空题
-
1. 2的相反数是 ．2. 使代数式 有意义的x取值范围是 ．3. 四边形ABCD是某个圆的内接四边形，若∠A=100°，则∠C= ．
4.如图，直线CD∥BF，直线AB与CD、EF分别相交于点M、N，若∠1=30°，则∠2= ．
5. 某地区今年参加初中毕业学业考试的九年级考生人数为31000人，数据31000人用科学记数法表示为人．6. 分解因式：x2﹣4x+4= ．
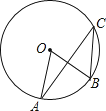
7.如图，在⊙O中，圆心角∠AOB=70°，那么圆周角∠C= ．
8.如图，已知菱形ABCD的两条对角线长分别为AC=8和BD=6，那么，菱形ABCD的面积为 ．
二、选择题
-
9. 一组数据1，8，5，3，3的中位数是（ ）A、3 B、3.5 C、4 D、510. 下列图形中，是轴对称图形但不是中心对称图形的是（ ）A、平行四边形 B、等腰三角形 C、矩形 D、正方形11. 下列说法错误的是（ ）A、对角线互相平分的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、一组对边相等，另一组对边平行的四边形是平行四边形12. 计算 ﹣ 的结果精确到0.01是（可用科学计算器计算或笔算）（ ）
A、0.30 B、0.31 C、0.32 D、0.3313. 不等式组 的解集是（ ）A、x＞1 B、1＜x≤2 C、x≤2 D、无解14. 一个等腰三角形一边长为4cm，另一边长为5cm，那么这个等腰三角形的周长是（ ）A、13cm B、14cm C、13cm或14cm D、以上都不对15. 在一个不透明的口袋中装有6个红球，2个绿球，这些球除颜色外无其他差别，从这个袋子中随机摸出一个球，摸到红球的概率为（ ）
A、 B、 C、 D、116. 一次函数y=﹣2x+3的图象不经过的象限是（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限17.如图，在△ABC中，DE∥BC，DB=2AD，△ADE的面积为1，则四边形DBCE的面积为（ ）
A、3 B、5 C、6 D、818. 在Rt△ABC中，∠C=90°，BC=3cm，AC=4cm，以点C为圆心，以2.5cm为半径画圆，则⊙C与直线AB的位置关系是（ ）A、相交 B、相切 C、相离 D、不能确定三、解答题
-
19. 计算：（ ﹣3）0﹣2sin30°﹣ ．20. 先化简，再求值：（a+b）（a﹣b）﹣b（a﹣b），其中，a=﹣2，b=1．21.
如图，点O是线段AB和线段CD的中点．
(1)、求证：△AOD≌△BOC；(2)、求证：AD∥BC．22.如图，已知反比例函数y= 的图象与直线y=﹣x+b都经过点A（1，4），且该直线与x轴的交点为B．
(1)、求反比例函数和直线的解析式；(2)、求△AOB的面积23.某校为了了解学生家长对孩子用手机的态度问题，随机抽取了100名家长进行问卷调查，每位学生家长只有一份问卷，且每份问卷仅表明一种态度（这100名家长的问卷真实有效），将这100份问卷进行回收整理后，绘制了如下两幅不完整的统计图．
(1)、“从来不管”的问卷有份，在扇形图中“严加干涉”的问卷对应的圆心角为 ．(2)、请把条形图补充完整．(3)、若该校共有学生2000名，请估计该校对手机问题“严加干涉”的家长有多少人．24.测量计算是日常生活中常见的问题，如图，建筑物BC的屋顶有一根旗杆AB，从地面上D点处观测旗杆顶点A的仰角为50°，观测旗杆底部B点的仰角为45°，（可用的参考数据：sin50°≈0.8，tan50°≈1.2）
(1)、若已知CD=20米，求建筑物BC的高度；(2)、若已知旗杆的高度AB=5米，求建筑物BC的高度．25. 某商店购进甲乙两种商品，甲的进货单价比乙的进货单价高20元，已知20个甲商品的进货总价与25个乙商品的进货总价相同．(1)、求甲、乙每个商品的进货单价；(2)、若甲、乙两种商品共进货100件，要求两种商品的进货总价不高于9000元，同时甲商品按进价提高10%后的价格销售，乙商品按进价提高25%后的价格销售，两种商品全部售完后的销售总额不低于10480元，问有哪几种进货方案？(3)、在条件（2）下，并且不再考虑其他因素，若甲乙两种商品全部售完，哪种方案利润最大？最大利润是多少？26.如图，长方形OABC的OA边在x轴的正半轴上，OC在y轴的正半轴上，抛物线y=ax2+bx经过点B（1，4）和点E（3，0）两点．
(1)、求抛物线的解析式；(2)、若点D在线段OC上，且BD⊥DE，BD=DE，求D点的坐标；(3)、在条件（2）下，在抛物线的对称轴上找一点M，使得△BDM的周长为最小，并求△BDM周长的最小值及此时点M的坐标；(4)、在条件（2）下，从B点到E点这段抛物线的图象上，是否存在一个点P，使得△PAD的面积最大？若存在，请求出△PAD面积的最大值及此时P点的坐标；若不存在，请说明理由．