2016年湖南省邵阳市中考数学试卷

试卷更新日期：2016-07-05 类型：中考真卷

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分

1. ﹣ $\sqrt{2}$ 的相反数是（　　）

A、 $\sqrt{2}$ B、﹣ $\frac{\sqrt{2}}{2}$ C、﹣ $\sqrt{2}$ D、﹣2

查看试题解析
2. 下面四个手机应用图标中是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3.
如图所示，直线AB、CD被直线EF所截，若AB∥CD，∠1=100°，则∠2的大小是（　　）

A、10° B、50° C、80° D、100°

查看试题解析
4.
在学校演讲比赛中，10名选手的成绩统计图如图所示，则这10名选手成绩的众数是（　　）

A、95 B、90 C、85 D、80

查看试题解析
5. 一次函数y=﹣x+2的图象不经过的象限是（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 分式方程 $\frac{3}{x}$ = $\frac{4}{x + 1}$ 的解是（　　）

A、x=﹣1 B、x=1 C、x=2 D、x=3

查看试题解析
7. 一元二次方程2x²﹣3x+1=0的根的情况是（　　）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
8.
如图所示，点D是△ABC的边AC上一点（不含端点），AD=BD，则下列结论正确的是（　　）

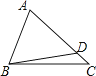A、AC＞BC B、AC=BC C、∠A＞∠ABC D、∠A=∠ABC

查看试题解析
9.
如图所示，AB是⊙O的直径，点C为⊙O外一点，CA，CD是⊙O的切线，A，D为切点，连接BD，AD．若∠ACD=30°，则∠DBA的大小是（　　）

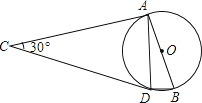A、15° B、30° C、60° D、75°

查看试题解析
10.
如图所示，下列各三角形中的三个数之间均具有相同的规律，根据此规律，最后一个三角形中y与n之间的关系是（　　）

A、y=2n+1 B、y=2ⁿ+n C、y=2ⁿ⁺¹+n D、y=2ⁿ+n+1

查看试题解析

二、填空题：本大题共8小题，每小题3分，共24分

11. 将多项式m³﹣mn²因式分解的结果是．

查看试题解析
12. 学校射击队计划从甲、乙两人中选拔一人参加运动会射击比赛，在选拔过程中，每人射击10次，计算他们的平均成绩及方差如下表：
选手
甲
乙
平均数（环）
9.5
9.5
方差
0.035
0.015
请你根据上表中的数据选一人参加比赛，最适合的人选是．

查看试题解析
13.
将等边△CBA绕点C顺时针旋转∠α得到△CB′A′，使得B，C，A′三点在同一直线上，如图所示，则∠α的大小是．

查看试题解析
14.
已知反比例函数y= $\frac{k}{x}$ （k≠0）的图象如图所示，则k的值可能是（写一个即可）．

查看试题解析
15. 不等式组 ${\begin{cases} x - 1 \leq 0 \\ 5 x > 3 x - 4 \end{cases}$ 的解集是．

查看试题解析
16.
2015年7月，第四十五届“世界超级计算机500强排行榜”榜单发布，我国国防科技大学研制的“天河二号”以每秒3386×10¹³次的浮点运算速度第五次蝉联冠军，若将3386×10¹³用科学记数法表示成a×10ⁿ的形式，则n的值是．

查看试题解析
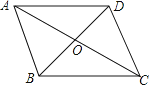
17.
如图所示，四边形ABCD的对角线相交于点O，若AB∥CD，请添加一个条件（写一个即可），使四边形ABCD是平行四边形．

查看试题解析
18.
如图所示，在3×3的方格纸中，每个小方格都是边长为1的正方形，点O，A，B均为格点，则扇形OAB的面积大小是．

查看试题解析

三、解答题：本大题共3小题，每小题8分，共24分

19. 计算：（﹣2）²+2cos60°﹣（ $\sqrt{5} - π$ ）⁰ ．

查看试题解析
20. 先化简，再求值：（m﹣n）²﹣m（m﹣2n），其中m= $\sqrt{3}$ ，n= $\sqrt{2}$ ．

查看试题解析
21.
如图所示，点E，F是平行四边形ABCD对角线BD上的点，BF=DE，求证：AE=CF．

查看试题解析

四、解答题：本大题共3小题，每小题8分，共24分

22.
如图为放置在水平桌面上的台灯的平面示意图，灯臂AO长为40cm，与水平面所形成的夹角∠OAM为75°．由光源O射出的边缘光线OC，OB与水平面所形成的夹角∠OCA，∠OBA分别为90°和30°，求该台灯照亮水平面的宽度BC（不考虑其他因素，结果精确到0.1cm．温馨提示：sin75°≈0.97，cos75°≈0.26， $\sqrt{3} \approx 1.73$ ）．

查看试题解析
23.
为了响应“足球进校园”的目标，某校计划为学校足球队购买一批足球，已知购买2个A品牌的足球和3个B品牌的足球共需380元；购买4个A品牌的足球和2个B品牌的足球共需360元．

(1)、求A，B两种品牌的足球的单价．

(2)、求该校购买20个A品牌的足球和2个B品牌的足球的总费用．

查看试题解析
24.
为了解市民对全市创卫工作的满意程度，某中学教学兴趣小组在全市甲、乙两个区内进行了调查统计，将调查结果分为不满意，一般，满意，非常满意四类，回收、整理好全部问卷后，得到下列不完整的统计图．

请结合图中信息，解决下列问题：

(1)、求此次调查中接受调查的人数．

(2)、求此次调查中结果为非常满意的人数．

(3)、兴趣小组准备从调查结果为不满意的4位市民中随机选择2为进行回访，已知4为市民中有2位来自甲区，另2位来自乙区，请用列表或用画树状图的方法求出选择的市民均来自甲区的概率．

查看试题解析

五、综合题：本大题共2小题，其中25题8分，26题10分，共18分

25.
尤秀同学遇到了这样一个问题：如图1所示，已知AF，BE是△ABC的中线，且AF⊥BE，垂足为P，设BC=a，AC=b，AB=c．
求证：a²+b²=5c²
该同学仔细分析后，得到如下解题思路：
先连接EF，利用EF为△ABC的中位线得到△EPF∽△BPA，故 $\frac{E P}{B P} = \frac{P F}{P A} = \frac{E F}{B A} = \frac{1}{2}$ ，设PF=m，PE=n，用m，n把PA，PB分别表示出来，再在Rt△APE，Rt△BPF中利用勾股定理计算，消去m，n即可得证

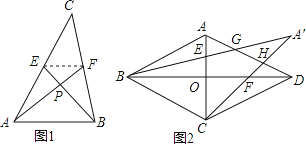(1)、请你根据以上解题思路帮尤秀同学写出证明过程．

(2)、
利用题中的结论，解答下列问题：在边长为3的菱形ABCD中，O为对角线AC，BD的交点，E，F分别为线段AO，DO的中点，连接BE，CF并延长交于点M，BM，CM分别交AD于点G，H，如图2所示，求MG²+MH²的值．

查看试题解析
26.
已知抛物线y=ax²﹣4a（a＞0）与x轴相交于A，B两点（点A在点B的左侧），点P是抛物线上一点，且PB=AB，∠PBA=120°，如图所示．

(1)、求抛物线的解析式．

(2)、设点M（m，n）为抛物线上的一个动点，且在曲线PA上移动．
①当点M在曲线PB之间（含端点）移动时，是否存在点M使△APM的面积为 $\frac{5 \sqrt{3}}{2}$ ？若存在，求点M的坐标；若不存在，请说明理由．
②当点M在曲线BA之间（含端点）移动时，求|m|+|n|的最大值及取得最大值时点M的坐标．

查看试题解析

选手	甲	乙
平均数（环）	9.5	9.5
方差	0.035	0.015