2016年湖南省衡阳市中考数学试卷

试卷更新日期：2016-07-05 类型：中考真卷

进入 出卷网 下载

一、选择题（共12小题，每小题3分，满分36分）

  • 1. ﹣4的相反数是（　　）

    A、﹣ 14 B、14 C、﹣4 D、4

    查看试题解析

  • 2. 如果分式 3x−1 有意义，则x的取值范围是（　　）

    A、全体实数 B、x≠1 C、x=1 D、x＞1

    查看试题解析

  • 3.

    如图，直线AB∥CD，∠B=50°，∠C=40°，则∠E等于（　　）


    A、70° B、80° C、90° D、100°

    查看试题解析

  • 4. 下列几何体中，哪一个几何体的三视图完全相同（　　）

    A、球体 B、圆柱体 C、四棱锥 D、圆锥

    查看试题解析

  • 5. 下列各式中，计算正确的是（　　）

    A、3x+5y=8xy B、x3•x5=x8 C、x6÷x3=x2 D、（﹣x3）3=x6

    查看试题解析

  • 6. 为缓解中低收入人群和新参加工作的大学生住房的需求，某市将新建保障住房3600000套，把3600000用科学记数法表示应是（　　）

    A、0.36×107 B、3.6×106 C、3.6×107 D、36×105

    查看试题解析

  • 7. 要判断一个学生的数学考试成绩是否稳定，那么需要知道他最近连续几次数学考试成绩的（　　）

    A、平均数 B、中位数 C、众数 D、方差

    查看试题解析

  • 8. 正多边形的一个内角是150°，则这个正多边形的边数为（　　）

    A、10 B、11 C、12 D、13

    查看试题解析

  • 9. 随着居民经济收入的不断提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，抽样调查显示，截止2015年底某市汽车拥有量为16.9万辆．已知2013年底该市汽车拥有量为10万辆，设2013年底至2015年底该市汽车拥有量的平均增长率为x，根据题意列方程得（　　）

    A、10（1+x）2=16.9 B、10（1+2x）=16.9 C、10（1﹣x）2=16.9 D、10（1﹣2x）=16.9

    查看试题解析

  • 10. 关于x的一元二次方程x2+4x+k=0有两个相等的实根，则k的值为（　　）

    A、k=﹣4 B、k=4 C、k≥﹣4 D、k≥4

    查看试题解析

  • 11. 下列命题是假命题的是（　　）

    A、经过两点有且只有一条直线 B、三角形的中位线平行且等于第三边的一半 C、平行四边形的对角线相等 D、圆的切线垂直于经过切点的半径

    查看试题解析

  • 12.

    如图，已知A，B是反比例函数y= kx （k＞0，x＞0）图象上的两点，BC∥x轴，交y轴于点C，动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过P作PM⊥x轴，垂足为M．设三角形OMP的面积为S，P点运动时间为t，则S关于x的函数图象大致为（　　）


    A、 B、 C、 D、

    查看试题解析

二、填空题（共6小题，每小题3分，满分18分）

  • 13. 因式分解：a2+ab= ．

    查看试题解析

  • 14. 计算： xx−1 ﹣ 1x−1 = ．

    查看试题解析

  • 15. 点P（x﹣2，x+3）在第一象限，则x的取值范围是 ．

    查看试题解析

  • 16. 若△ABC与△DEF相似且面积之比为25：16，则△ABC与△DEF的周长之比为 ．

    查看试题解析

  • 17. 若圆锥底面圆的周长为8π，侧面展开图的圆心角为90°，则该圆锥的母线长为 ．

    查看试题解析

  • 18.

    如图所示，1条直线将平面分成2个部分，2条直线最多可将平面分成4个部分，3条直线最多可将平面分成7个部分，4条直线最多可将平面分成11个部分．现有n条直线最多可将平面分成56个部分，则n的值为 ．

    查看试题解析

三、解答题（共8小题，满分66分）

  • 19. 先化简，再求值：（a+b）（a﹣b）+（a+b）2 ， 其中a=﹣1，b= 12 ．

    查看试题解析

  • 20.

    为庆祝建党95周年，某校团委计划在“七一”前夕举行“唱响红歌”班级歌咏比赛，要确定一首喜欢人数最多的歌曲为每班必唱歌曲．为此提供代号为A，B，C，D四首备选曲目让学生选择，经过抽样调查，并将采集的数据绘制如下两幅不完整的统计图．请根据图①，图②所提供的信息，解答下列问题：


    (1)、本次抽样调查中，选择曲目代号为A的学生占抽样总数的百分比为；

    (2)、请将图②补充完整；

    (3)、若该校共有1530名学生，根据抽样调查的结果估计全校共有多少学生选择此必唱歌曲？（要有解答过程）

    查看试题解析

  • 21.

    如图，点A、C、D、B四点共线，且AC=BD，∠A=∠B，∠ADE=∠BCF，求证：DE=CF．

    查看试题解析

  • 22.

    在四张背面完全相同的纸牌A、B、C、D，其中正面分别画有四个不同的几何图形（如图），小华将这4张纸牌背面朝上洗匀后摸出一张，放回洗匀后再摸一张．


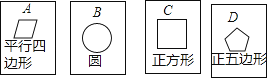    (1)、用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌可用A、B、C、D表示）；

    (2)、求摸出两张纸牌牌面上所画几何图形，既是轴对称图形又是中心对称图形的概率．

    查看试题解析

  • 23. 为保障我国海外维和部队官兵的生活，现需通过A港口、B港口分别运送100吨和50吨生活物资．已知该物资在甲仓库存有80吨，乙仓库存有70吨，若从甲、乙两仓库运送物资到港口的费用（元/吨）如表所示：

    港口

    运费（元/台）

    甲库

    乙库

    A港

    14

    20

    B港

    10

    8

    (1)、设从甲仓库运送到A港口的物资为x吨，求总运费y（元）与x（吨）之间的函数关系式，并写出x的取值范围；

    (2)、求出最低费用，并说明费用最低时的调配方案．

    查看试题解析

  • 24.

    在某次海上军事学习期间，我军为确保△OBC海域内的安全，特派遣三艘军舰分别在O、B、C处监控△OBC海域，在雷达显示图上，军舰B在军舰O的正东方向80海里处，军舰C在军舰B的正北方向60海里处，三艘军舰上装载有相同的探测雷达，雷达的有效探测范围是半径为r的圆形区域．（只考虑在海平面上的探测）


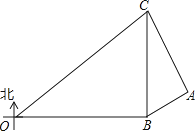    (1)、若三艘军舰要对△OBC海域进行无盲点监控，则雷达的有效探测半径r至少为多少海里？

    (2)、现有一艘敌舰A从东部接近△OBC海域，在某一时刻军舰B测得A位于北偏东60°方向上，同时军舰C测得A位于南偏东30°方向上，求此时敌舰A离△OBC海域的最短距离为多少海里？

    (3)、若敌舰A沿最短距离的路线以20 2 海里/小时的速度靠近△OBC海域，我军军舰B沿北偏东15°的方向行进拦截，问B军舰速度至少为多少才能在此方向上拦截到敌舰A？

    查看试题解析

  • 25.

    在平面直角坐标中，△ABC三个顶点坐标为A（﹣ 3 ，0）、B（ 3 ，0）、C（0，3）．


    (1)、求△ABC内切圆⊙D的半径．

    (2)、过点E（0，﹣1）的直线与⊙D相切于点F（点F在第一象限），求直线EF的解析式．

    (3)、以（2）为条件，P为直线EF上一点，以P为圆心，以2 7 为半径作⊙P．若⊙P上存在一点到△ABC三个顶点的距离相等，求此时圆心P的坐标．

    查看试题解析

  • 26.

    如图，抛物线y=ax2+bx+c经过△ABC的三个顶点，与y轴相交于（0， 94 ），点A坐标为（﹣1，2），点B是点A关于y轴的对称点，点C在x轴的正半轴上．


    (1)、求该抛物线的函数关系表达式．

    (2)、点F为线段AC上一动点，过F作FE⊥x轴，FG⊥y轴，垂足分别为E、G，当四边形OEFG为正方形时，求出F点的坐标．

    (3)、将（2）中的正方形OEFG沿OC向右平移，记平移中的正方形OEFG为正方形DEFG，当点E和点C重合时停止运动，设平移的距离为t，正方形的边EF与AC交于点M，DG所在的直线与AC交于点N，连接DM，是否存在这样的t，使△DMN是等腰三角形？若存在，求t的值；若不存在请说明理由．

    查看试题解析