安徽安庆四中2020-2021学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-01-08 类型:月考试卷
一、单选题
-
1. 下列各式中,y是x的二次函数的是( )A、 B、 C、 D、2. 在同一坐标系内,函数y=kx2和y=kx+2(k≠0)的图象大致如图( )A、
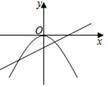 B、
B、 C、
C、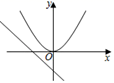 D、
D、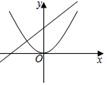 3. 抛物线 的顶点坐标为( )A、 B、 C、 D、4. 在反比例函数 图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )A、k>3 B、k>0 C、k<3 D、k<05. 将二次函数y=5x2的图象先向右平移2个单位,再向下平移3个单位,得到的函数图象的解析式为( )A、y=5(x+2)2+3 B、y=5(x﹣2)2+3 C、y=5(x+2)2﹣3 D、y=5(x﹣2)2﹣36. 对于抛物线 的说法错误的是( )A、抛物线的开口向下 B、抛物线的顶点坐标是(1,-3) C、抛物线的对称轴是直线 D、当 时, 随 的增大而增大7. 如图,抛物线 的对称轴是直线 ,且经过点 ,则下列结论中正确的是( )
3. 抛物线 的顶点坐标为( )A、 B、 C、 D、4. 在反比例函数 图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )A、k>3 B、k>0 C、k<3 D、k<05. 将二次函数y=5x2的图象先向右平移2个单位,再向下平移3个单位,得到的函数图象的解析式为( )A、y=5(x+2)2+3 B、y=5(x﹣2)2+3 C、y=5(x+2)2﹣3 D、y=5(x﹣2)2﹣36. 对于抛物线 的说法错误的是( )A、抛物线的开口向下 B、抛物线的顶点坐标是(1,-3) C、抛物线的对称轴是直线 D、当 时, 随 的增大而增大7. 如图,抛物线 的对称轴是直线 ,且经过点 ,则下列结论中正确的是( ) A、 B、 C、 D、8. 若二次的数 的x与y的部分对应值如下表:
A、 B、 C、 D、8. 若二次的数 的x与y的部分对应值如下表:x
-7
-6
-5
-4
-3
-2
y
-27
-13
-3
3
5
3
则当 时,y的值为( )
A、5 B、-3 C、-13 D、-279. 如图,菱形OABC的顶点A的坐标为(3,4),顶点C在x轴的正半轴上,反比例函数y= (x>0)的图象经过顶点B,则反比例函数的表达式为( )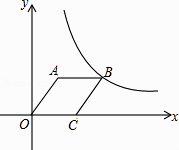 A、y= B、y= C、y= D、y=10. 如图,点A,B的坐标分别为(1,4)和(4,4),抛物线 的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为( )
A、y= B、y= C、y= D、y=10. 如图,点A,B的坐标分别为(1,4)和(4,4),抛物线 的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为( ) A、-3 B、1 C、5 D、8
A、-3 B、1 C、5 D、8二、填空题
-
11. 抛物线 的对称轴是直线 .12. 二次函数 与x轴的两个交点的横坐标分别为m和n , 且 ,则a , b , m , n四个数的大小关系是(用<号连接)13. 已知点A的坐标为 ,点B的坐标为 ,点P在函数 的图象上,如果 的面积是6,则点P的坐标是 .14. 如图,在平面直角坐标系中,平行四边形OABC的顶点A在反比例函数 上,顶点B在反比例函数 上,点C在x轴的正半轴上,则平行四边形OABC的面积是 .

三、解答题
-
15. 如图:一次函数的图象与反比例函数 的图象交于A(-2,6)和点B(4,n)
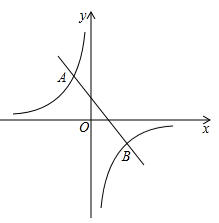 (1)、求反比例函数的解析式和B点坐标(2)、根据图象回答,在什么范围时,一次函数的值大于反比例函数的值.16. 如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形 和 ,求DE长的最小值.
(1)、求反比例函数的解析式和B点坐标(2)、根据图象回答,在什么范围时,一次函数的值大于反比例函数的值.16. 如图,线段AB的长为2,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形 和 ,求DE长的最小值.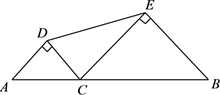 17. 某黄金珠宝商店,今年4月份以前,每天的进货量与销售量均为1000克,进入4月份后,每天的进货量保持不变,因国际金价大跌走熊,市场需求量不断增加.如图是4月前后一段时期库存量
17. 某黄金珠宝商店,今年4月份以前,每天的进货量与销售量均为1000克,进入4月份后,每天的进货量保持不变,因国际金价大跌走熊,市场需求量不断增加.如图是4月前后一段时期库存量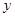 (克)与销售时间
(克)与销售时间  (月份)之间的函数图象. (4月份以30天计算)
(月份)之间的函数图象. (4月份以30天计算) 
商品名称
金 额
A
B
投资金额x(万元)
x
5
x
1
5
销售收入y(万元)
y1=kx
(k≠0)
3
y2=ax2+bx(a≠0)
2.8
10
(1)、该商店月份开始出现供不应求的现象,4月份的平均日销售量为克?(2)、为满足市场需求,商店准备投资20万元同时购进A、B两种新黄金产品.其中购买A、B两种新黄金产品所投资的金额与销售收入存在如图所示的函数对应关系. 请你判断商店这次投资能否盈利?(3)、在(2)的其他条件不变的情况下,商店准备投资m万元同时购进A、B两种新黄金产品,并实现最大盈利3.2万元,请求出m的值.(利润=销售收入-投资金额)18. 按图所示的流程,输入一个数据x,根据y与x的关系式就输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20~100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(a)新数据都在60~100(含60和100)之间;
(b)新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大.
(1)、若y与x的关系是y=x+p(100-x),请说明:当p= 时,这种变换满足上述两个要求;(2)、若按关系式y=a(x-h)2+k (a>0)将数据进行变换,请写出一个满足上述要求的这种关系式.(不要求对关系式符合题意作说明,但要写出关系式得出的主要过程)