广东省深圳市2020-2021学年九年级上学期数学期中试卷
试卷更新日期：2021-01-06 类型：期中考试
一、选择题(本大题共10小题，每小题3分，共30分)
-
1. 方程x2=16的解为（ ）A、x=4 B、x=-4 C、x=4或-4 D、x=0或42. 如图1，转盘中四个扇形的面积都相等，小明随意转动转盘1次，指针指向的数字为偶数的概率为（ ）
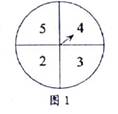A、 B、 C、 D、3. 已知 ，若b+d+f=9，则a+c+e=（ ）A、12 B、15 C、16 D、184. 如图2，以点O为位似中心，画一个四边形A'B'C'D'，使它与四边形ABCD位似，且相似比为 ，则下列说法错误的是（ ）
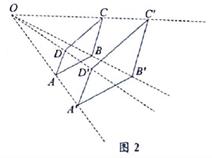A、四边形ABCD∽四边形A'B'C'D' B、点C，O，C' 三点在同一直线上 C、 D、OB= OB'5. ABCD添加下列条件后，仍不能使它成为矩形的是（ ）A、AB⊥BC B、AC=BD C、∠A=∠B D、BC= CD6. 将一元二次方程x2+4x+2= 0配方后可得到方程（ ）A、(x-2)2=2 B、(x+2)2=2 C、(x-2)2=6 D、(x+2)2=67. 下列说法正确的是（ ）A、已知线段AB=2，点C是AB的黄金分割点(AC>BC)，则AC= -1 B、相似三角形的面积之比等于它们的相似比 C、对角线相等且垂直的四边形是正方形 D、方程x2+3x+4=0有两个实数解8. 如图3，在 ABCD中，按如下步骤作图：①以A为圆心，AB长为半径画弧交AD于F；②连接BF，分别以点B，F为圆心，以大于 BF的长为半径作弧，两弧交于点G；③作射线AG交BC于点E。若BF=6，AB=5，则AE的长为（ ）
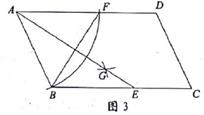A、6 B、7 C、8 D、99. 已知m是一元二次方程x2-x-3=0的根，则代数式2m2-2m+7的值是（ ）A、11 B、12 C、13 D、1410. 如图4，矩形ABCD绕点A逆时针旋转90*得矩形AEFG，连接CF，交AD于点P，M是CF的中点，连接AM，交EF于点Q。则下列结论：
①AM⊥CF；②△CDP≌△AEQ ；③连接PQ，则PQ= MQ；④若AB=2，BC=6，则MQ= 其中，正确结论的个数有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题(本大题共5小题，每小题3分，共15分)
-
11. 因式分解：x2-6x+9=12. 一个不透明的袋子中有红球和黑球共25个，这些球除颜色外都相同．将袋子中的球搅拌均匀，从中随机摸出一个球，记下它的颜色再放回袋子中．不断重复这一过程，共摸了400次球，发现有240次摸到黑球，由此估计袋中的黑球大约有个。13. 如图5，已知直线l1∥l2∥l3 ， 直线m与直线l1 ， l2 ， l3分别交于A，D，F：直线n与直线l1 ， l2 ， l3分别交于B，C，E。若 ，则 =。
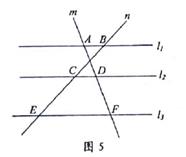14. 对于实数a，b，定义运算“ ”： a b=a2-5a+2b，例如： 4 3=42-5×4+2×3=2。根据此定义，则方程x 3=0的根为。15. 如图6，AD是△ABC的角平分线，CE是△ABC的中线，AD，CE交于点F，若∠1=∠B，则 =。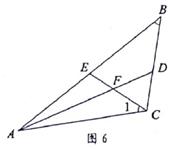
三、解答题(本大题共7小题，其中第16题5分，第17题6分，第18题8分，第19题8分，第20题8分，第21题10分，第22题10分，共55分)
-
16. 计算：(2020-π)0+|1- |- +( )-117. 解下列方程：(1)、x2=3x；(2)、2x2-4x-1=018. 自深圳经济特区建立至今40年以来，深圳本土诞生了许多优秀的科技企业。华为、腾讯、中兴、大疆就是其中的四个杰出代表．某数学兴趣小组在校内对这四个企业进行“你最认可的特区科技企业”调查活动．兴趣小组随机调查了m人(每人必选一个且只能选一个)，并将调查结果绘制成了如下尚不完整的统计图，请根据图中信息回答以下问题：
(1)、请将以上两个统计图补充完整；(2)、m= ，“腾讯”所在扇形的圆心角的度数为 ；(3)、该校共有2000名同学，估计最认可“华为”的同学大约有名；(4)、已知A，B两名同学都最认可“华为”，C同学最认可“腾讯”，D同学最认可“中兴”，从这四名同学中随机抽取两名同学，请你利用画树状图或列表的方法，求出这两名同学最认可的特区科技企业不一样的概率。19. 如图7，在▱ABCD中，AD的垂直平分线经过点B，与CD的延长线交于点E，AD。BE相交于点O，连接AE，BD。
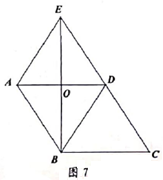(1)、求证：四边形ABDE为菱形；(2)、若AD=8，问在BC上是否存在点P，使得PE+PD最小？若存在，求线段BP的长；若不存在，请说明理由。20. 某超市销售一种进价为40元/件的衬衫。若以50元/件销售，一个月能售出500件，据市场分析，这种衬衫的售价每上涨1元，月销量就会减少10件。现在超市要求月销售利润为8000元，且售价不超过70元，这种衬衫的售价应定为多少？21. 如图，在△ABC中，AB=AC=6，BC=2，过点A作AM∥BC，点P是AB上一点，作∠CPD=∠B，PD交AM于点D。
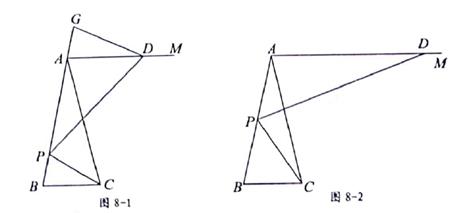(1)、如图8-1，在BA的延长线上取点G，使得DG=DA，则 的值为；(2)、如图8-1，在(1)的条件下，求证：△DGP∽△PBC ；(3)、如图8-2，当点P是AB的中点时，求AD的长。22. 如图，矩形AOBC的顶点B， A分别在x轴，y轴上，点C坐标是(5，4)，D为BC边上一点，将矩形沿AD折叠，点C落在x轴上的点E处，AD的延长线与x轴相交于点F。
(1)、如图9-1，求点D的坐标；(2)、如图9-2，若P是AF上一动点，PM⊥AC交AC于M，PN⊥CF交CF于N，设AP=t， FN=s，求s与t之间的函数关系式；(3)、在(2)的条件下，是否存在点P，使△PMN为等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由。