福建省厦门市同安区2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2021-01-06 类型:期中考试
一、单选题
-
1. 已知一个一元二次方程的二次项系数是3,常数项是1,则这个方程可能是( )A、 B、 C、 D、2. 在平面直角坐标系中,点(2,6)关于原点对称的点的坐标是( )A、(-2,-6) B、(-2,6) C、(-6,2) D、(6,2)3. 下列图形中,不是中心对称图形的是( )A、线段 B、平行四边形 C、圆 D、等边三角形4. 如果将抛物线 向下平移1个单位,那么所得新抛物线的表达式是( )
A、 B、 C、 D、5. 如图,C是⊙O上一点,O是圆心,若∠C=35°,则∠AOB的度数为( ) A、35° B、70° C、105° D、150°6. 方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、有且只有一个实数根 D、没有实数根7. 如图,将△ABC绕点A逆时针旋转110°,得到△ADE , 若点D落在线段BC的延长线上,则∠B大小为( )
A、35° B、70° C、105° D、150°6. 方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、有且只有一个实数根 D、没有实数根7. 如图,将△ABC绕点A逆时针旋转110°,得到△ADE , 若点D落在线段BC的延长线上,则∠B大小为( )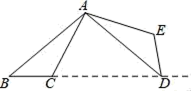 A、30° B、35° C、40° D、45°8. 新冠肺炎是一种传染性极强的疾病,如果有一人患病,经过两轮传染后有81人患病,设每轮传染中平均一个人传染了x个人,下列列式正确的是( )A、 B、 C、 D、9. 已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
A、30° B、35° C、40° D、45°8. 新冠肺炎是一种传染性极强的疾病,如果有一人患病,经过两轮传染后有81人患病,设每轮传染中平均一个人传染了x个人,下列列式正确的是( )A、 B、 C、 D、9. 已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:x
…
﹣1
0
1
2
3
…
y
…
10
5
2
1
2
…
则当y<5时,x的取值范围为( )
A、0<x<4 B、﹣4<x<4 C、x<﹣4或x>4 D、x>410. 如图,AB切⊙O于点B , OA与⊙O相交于点C , AC=CO , 点D为 上任意一点(不与点B、C重合),则∠BDC等于( ) A、120° B、130° C、140° D、150
A、120° B、130° C、140° D、150二、填空题
-
11. 方程 的解是 .12. 二次函数 的最小值是 .13. 如图,正六边形ABCDEF内接于 ,半径为4,则这个正六边形的边心距OM的长为 .
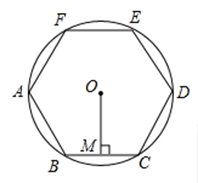 14. 在平面直角坐标系中,把点A(2,1)绕着原点顺时针旋转90°,得到的点B坐标为 .15. “圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”此问题的实质就是解决下面的问题:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长”.根据题意可得CD的长为 .
14. 在平面直角坐标系中,把点A(2,1)绕着原点顺时针旋转90°,得到的点B坐标为 .15. “圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何”此问题的实质就是解决下面的问题:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长”.根据题意可得CD的长为 .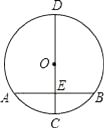 16. 已知点 、 、 都在二次函数 的图象上,若 ,则 、 、 的大小关系是 .
16. 已知点 、 、 都在二次函数 的图象上,若 ,则 、 、 的大小关系是 .三、解答题
-
17.(1)、(2)、18. 已知抛物线的顶点坐标为 ,且经过点 ,求该抛物线的解析式,并在平面直角坐标系中画出该抛物线的图像.19. 如图,直线AB经过⊙O上的一点C , 并且OA=OB , CA=CB , 求证:直线AB是⊙O的切线.
 20. 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1 .
20. 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,其中点A(5,4),B(1,3),将△AOB绕点O逆时针旋转90°后得到△A1OB1 . (1)、画出△A1OB1;(2)、在旋转过程中点B所经过的路径长.21. 关于x的一元二次方程 .(1)、求证:方程总有两个实数根;(2)、若方程有一根小于1,求k的取值范围.22. 某书店销售儿童书刊,一天可出售20套,每套盈利40元.为了扩大销售,增加盈利,尽快减少库存,书店决定采取降价措施.若一套书每降价1元,平均每天可多出售2套.(1)、若要书店每天盈利1200元,则需降价多少元?(2)、设书店一天可获利润y元,当每套书降价多少元时,书店可获最大利润?最大利润为多少?23. 已知四边形ABCD内接于⊙O,∠DAB=90°.
(1)、画出△A1OB1;(2)、在旋转过程中点B所经过的路径长.21. 关于x的一元二次方程 .(1)、求证:方程总有两个实数根;(2)、若方程有一根小于1,求k的取值范围.22. 某书店销售儿童书刊,一天可出售20套,每套盈利40元.为了扩大销售,增加盈利,尽快减少库存,书店决定采取降价措施.若一套书每降价1元,平均每天可多出售2套.(1)、若要书店每天盈利1200元,则需降价多少元?(2)、设书店一天可获利润y元,当每套书降价多少元时,书店可获最大利润?最大利润为多少?23. 已知四边形ABCD内接于⊙O,∠DAB=90°.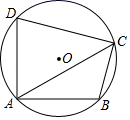 (1)、若AB=AD,求∠ACB的度数;(2)、连接AC,若AD=8,AB=6,对角线AC平分∠DAB,求AC的长.
(1)、若AB=AD,求∠ACB的度数;(2)、连接AC,若AD=8,AB=6,对角线AC平分∠DAB,求AC的长.
