福建省龙岩市永定区2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2021-01-06 类型:期中考试
一、单选题
-
1. 关于x的方程 ,有一个根为3,则m的值等于( )A、2 B、 C、-2 D、2. 三角形的两边长分别为3和6,第三边的长是方程 的一个根,则第三边的长是( )A、2 B、4 C、6 D、2或43. 如图,⊙O的直径长10,弦AB=8,M是弦AB上的动点,则OM的长的取值范围是( )
 A、3≤OM≤5 B、4≤OM≤5 C、3<OM<5 D、4<OM<54. 下表是满足二次函数 的五组数据, 是方程 的一个解,则下列选项中正确的是( )
A、3≤OM≤5 B、4≤OM≤5 C、3<OM<5 D、4<OM<54. 下表是满足二次函数 的五组数据, 是方程 的一个解,则下列选项中正确的是( )x
1.6
1.8
2.0
2.2
2.4
y
-0.80
-0.54
-0.20
0.22
0.2
A、 B、 C、 D、5. △ABC是⊙O内接三角形,∠BOC=80°,那么∠A等于( )A、80° B、40° C、140° D、40°或140°6. 下列图形中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 已知二次函数 的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数 的图象上,则下列结论正确的是( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y1<y2 D、y1<y3<y28. 已知圆锥的底面半径为1cm,母线长为3cm,则其侧面积为( )A、π B、2π C、3π D、4π9. 四边形 四个顶点的坐标分别为 ,则四边形 周长的最小值为( )A、12 B、 C、 D、10. 如图,直角坐标系中两点 ,P为线段 上一动点,作点B关于射线 的对称点C , 连接 ,则线段 的最小值为( )
7. 已知二次函数 的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数 的图象上,则下列结论正确的是( )A、y1<y2<y3 B、y2<y1<y3 C、y3<y1<y2 D、y1<y3<y28. 已知圆锥的底面半径为1cm,母线长为3cm,则其侧面积为( )A、π B、2π C、3π D、4π9. 四边形 四个顶点的坐标分别为 ,则四边形 周长的最小值为( )A、12 B、 C、 D、10. 如图,直角坐标系中两点 ,P为线段 上一动点,作点B关于射线 的对称点C , 连接 ,则线段 的最小值为( )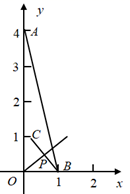 A、3 B、4 C、 D、
A、3 B、4 C、 D、二、填空题
-
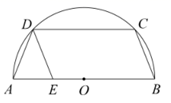
11. 方程x2=x的根是 .12. 边长为2的正方形ABCD的外接圆半径是 .13. 某商品成本为50元,由于连续两年降低成本,现为19元.若每年成本降低率相同,设成本降低率为x , 则所列方程为: .14. 定义运算: ,若 , 是方程 的两个根,则 的值为 .15. 如图, 的顶点B、C、D在半圆O上,顶点E在直径 上,连接 ,若 ,则 的度数为度.
 16. 在平面直角坐标系中,抛物线 经过 和 两点,直线 与抛物线交于A , B两点,P是直线 上方的抛物线上一动点,当 的面积最大值时,点P的横坐标为 .
16. 在平面直角坐标系中,抛物线 经过 和 两点,直线 与抛物线交于A , B两点,P是直线 上方的抛物线上一动点,当 的面积最大值时,点P的横坐标为 .三、解答题
-
17. 解方程: .18. 将矩形 绕点A顺时针旋转得到矩形 ,点 在 上.
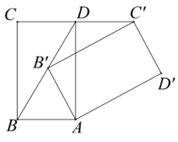
求证: .
19. 如图,点A、B、C、D、E都在⊙O上,AC平分∠BAD,且AB∥CE,求证:AD=CE.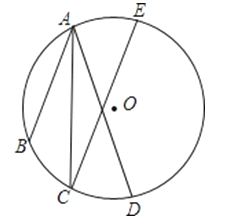 20. 已知关于 的方程 有两个不相等的实数根 .(1)、求k的取值范围;(2)、是否存在实数 ,使方程的两实根互为相反数?如果存在,求出 的值;如果不存在,请您说明理由.21. 如图,抛物线 经过点 ,交y轴于点C .
20. 已知关于 的方程 有两个不相等的实数根 .(1)、求k的取值范围;(2)、是否存在实数 ,使方程的两实根互为相反数?如果存在,求出 的值;如果不存在,请您说明理由.21. 如图,抛物线 经过点 ,交y轴于点C .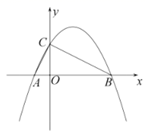 (1)、求抛物线的解析式(用一般式表示);(2)、若点E在抛物线上,且 是以 为底的等腰三角形,求点E的横坐标.22. 如图,AB为⊙O的直径,C、D为⊙O上的两个点, = = ,连接AD , 过点D作DE⊥AC交AC的延长线于点E .
(1)、求抛物线的解析式(用一般式表示);(2)、若点E在抛物线上,且 是以 为底的等腰三角形,求点E的横坐标.22. 如图,AB为⊙O的直径,C、D为⊙O上的两个点, = = ,连接AD , 过点D作DE⊥AC交AC的延长线于点E .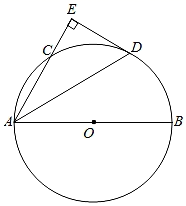 (1)、求证:DE是⊙O的切线.(2)、若直径AB=6,求AD的长.23. “互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为x元(x为正整数),每月的销售量为y条.(1)、直接写出y与x的函数关系式;(2)、设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?24.
(1)、求证:DE是⊙O的切线.(2)、若直径AB=6,求AD的长.23. “互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为x元(x为正整数),每月的销售量为y条.(1)、直接写出y与x的函数关系式;(2)、设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?24.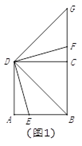
 (1)、如图1, 是正方形 边 上的一点,连接 ,将 绕着点 逆时针旋转90°,旋转后角的两边分别与射线 交于点 和点 .
(1)、如图1, 是正方形 边 上的一点,连接 ,将 绕着点 逆时针旋转90°,旋转后角的两边分别与射线 交于点 和点 .①线段 和 的数量关系是 ▲ ;
②写出线段 和 之间的数量关系.
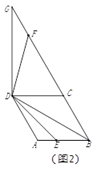
(2)、当四边形 为菱形, ,点 是菱形 边 所在直线上的一点,连接 ,将 绕着点 逆时针旋转120°,旋转后角的两边分别与射线 交于点 和点 .①如图2,点 在线段上时,请探究线段 和 之间的数量关系,写出结论并给出证明;
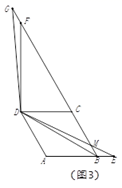
②如图3,点 在线段 的延长线上时, 交射线 于点 ;若 ,直接写出线段 的长度.
25. 已知抛物线 ,直线 与x轴交于点M , 与y轴交于点N .(1)、求证:抛物线与x轴必有公共点;(2)、若抛物线与x轴交于A、B两点,且抛物线的顶点C落在此直线上,求 的面积;(3)、若线段 与抛物线有且只有一个公共点,求m的取值范围.