福建省惠安县第二教学联盟2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-01-06 类型：期中考试

进入出卷网下载

一、单选题

1. 下列根式是最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{12}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{15}$

查看试题解析
2. 方程 $x^{2} - 25 = 0$ 的解是（）

A、 $x = 5$ B、 $x_{1} = 0, x_{2} = 25$ C、 $x_{1} = x_{2} = 5$ D、 $x_{1} = 5, x_{2} = - 5$

查看试题解析
3. 方程x²+4x﹣4=0 经过配方后，其结果正确的是（）

A、（x+2）²=4 B、（x﹣2）²=4 C、（x﹣2）²=8 D、（x+2）²=8

查看试题解析
4. 一元二次方程x²﹣2x+1＝0的根的情况是（　　）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
5. 现代互联网技术的广泛应用，促进快递行业高速发展，据调查，某家快递公司，今年5月份与7月份完成投递的快递总件数分别为8.5万件和10万件，设该快递公司这两个月投递总件数的月平均增长率为x，则下列方程正确的是（）

A、8.5（1+2x）=10 B、8.5（1+x）=10 C、8.5（1+x）²=10 D、8.5+8.5（1+x）+8.5（1+x）²=10

查看试题解析
6. 一张矩形纸片ABCD，已知AB＝3，AD＝2，小明按所给图步骤折叠纸片，则线段DG长为（）

A、2 $\sqrt{2}$ B、 $\sqrt{2}$ C、2 D、1

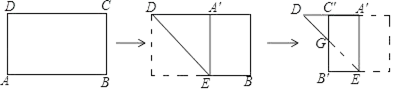查看试题解析
7. $△ A B C$ 的顶点A的坐标为(-2，4)，先将 $△ A B C$ 沿x轴对折，再向左平移两个单位，此时A点的坐标为（）

A、(2，-4) B、(0，-4) C、(-4，-4) D、(0，4)

查看试题解析
8. 已知 $\frac{a}{2} = \frac{b}{3} = \frac{c}{4} \neq 0$ ，a+2b=16，则c的值为（）

A、 $\frac{128}{7}$ B、 $\frac{64}{5}$ C、8 D、2

查看试题解析
9. 如图，在△ABC中，点G为△ABC的重心，过点G作DE∥BC，分别交AB、AC于点D、E，则△ADE与四边形DBCE的面积比为（　　）

A、 $\frac{4}{5}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、 $\frac{4}{9}$

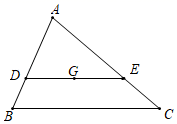查看试题解析
10. 如图，BD为矩形ABCD的对角线，将△BCD沿BD翻折得到 $△ B C^{'} D$ ， $B C^{'}$ 与边AD交于点E．若AB＝x₁ ， BC＝2x₂ ， DE＝3，其中x₁、x₂是关于x的方程x²﹣4x+m＝0的两个实根，则m的值是（）

A、 $\frac{16}{5}$ B、 $\frac{12}{5}$ C、3 D、2

查看试题解析

二、填空题

11. 要使二次根式 $\sqrt{x - 3}$ 有意义，则x的取值范围是．

查看试题解析
12. 已知关于x的方程x²+kx+3=0的一个根是 – 1，则k=.

查看试题解析
13. 如图，在△ABC中，AD，BE是两条中线，则S_△_EDC：S_△_ABC= ．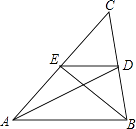

查看试题解析
14. 如图4，我国现代数学著作《九章算术》中有“井深几何”问题如下：今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？它的题意可以由如图所示获得，井深 $B C$ 为尺．

查看试题解析
15. 若一元二次方程ax²+bx+c=0中，4a﹣2b+c=0．则此方程必有一根为．

查看试题解析
16. 阅读以下的材料：
如果两个正数a ， b ，即a $>$ 0，b $>$ 0，则有下面的不等式： $\frac{a + b}{2} \geq \sqrt{a b}$ 当且仅当a=b时取到等号，我们把 $\frac{a + b}{2}$ 叫做正数a ， b的算术平均数，把 $\sqrt{a b}$ 叫做正数a ， b的几何平均数，于是上述不等式可表述为：两个正数的算术平均数不小于(即大于或等于)它们的几何平均数．它在数学中有广泛的应用，是解决最大(小)值问题的有力工具，下面举一例子：

例：已知x $>$ 0，求函数 $y = x + \frac{4}{x}$ 的最小值．

解：令 $a = x ， b = \frac{4}{x}$ ，则有 $a + b \geq 2 \sqrt{a b}$ ，得 $y = x + \frac{4}{x} \geq 2 \sqrt{x \cdot \frac{4}{x}} = 4$ ，当且仅当 $x = \frac{4}{x}$ 时，即x=2时，函数有最小值，最小值为4．

根据上面回答下列问题

①已知x $>$ 0，则当x=时，函数 $y = 2 x + \frac{3}{x}$ 取到最小值，最小值为；

②已知x $>$ 0，则自变量x取时，函数 $y = \frac{x}{x^{2} - 2 x + 9}$ 最大值是．

查看试题解析

三、解答题

17. 计算： $\sqrt{2} \times \sqrt{3} - \sqrt{24} + | - \sqrt{6} |$

查看试题解析
18. 解方程：x（x﹣5）+6=0

查看试题解析
19. 先化简，再求值： $(a - \sqrt{5}) (a + \sqrt{5}) + a (5 - a)$ ，其中 $a = \sqrt{5} + 1$ .

查看试题解析
20. 如图，在11×14的网格图中，△ABC三个顶点坐标分别为A（﹣4，1），B（﹣1，1），（﹣2，4）．

(1)、以A为位似中心，将△ABC放大为原来的2倍得到△AB₁C₁ ，请在网格图画出△AB₁C₁；

(2)、直接写出（1）中点B₁ ， C₁的坐标．

查看试题解析
21. 如图，在正方形ABCD中，点E、F、G 分别在AB、BC、CD上，且 $E F ⊥ F G$ 于F．

(1)、求证：△BEF∽△CFG；

(2)、若AB=12，AE=3，CF=4，求CG的长．

查看试题解析
22. 某单位准备组织员工到武夷山风景区旅游，旅行社给出了如下收费标准（如图所示）：

设参加旅游的员工人数为x人．

(1)、当25＜x＜40时，人均费用为元，当x≥40时，人均费用为元；

(2)、该单位共支付给旅行社旅游费用27000元，请问这次参加旅游的员工人数共有多少人？

查看试题解析
23. 如果关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 有两个实数根，且其中一个根为另一个根的 $2$ 倍，那么称这样的方程为“倍根方程”，例如，一元二次方程 $x^{2} - 6 x + 8 = 0$ 的两个根是 $2$ 和 $4$ ，则方程 $x^{2} - 6 x + 8 = 0$ 就是“倍根方程”．

(1)、若一元二次方程 $x^{2} - 3 x + c = 0$ 是“倍根方程”，则c＝．

(2)、若关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 是“倍根方程”，则 $a$ ， $b$ ， $c$ 之间的关系为．

(3)、若 $(x - 2) (m x - n) = 0 (m \neq 0)$ 是“倍根方程”，求代数式 $4 m^{2} - 5 m n + n^{2}$ 的值．

查看试题解析
24. 如图，在 $△$ ABC中，点D是BC边上的一个动点（不与B、C重合），BC=4 $\sqrt{3}$ ，∠B=∠ADE=∠C=30°．

(1)、求证：△ABD∽△DCE；

(2)、设BD=x，AE=y，求y关于x的函数关系式并写出自变量x的取值范围；

(3)、当△ADE是等腰三角形时，求AE的长．

查看试题解析
25. 如图，已知直线 $y = \frac{3}{4} x + b$ 与x轴、y轴分别交于点B、A，点P是y轴上一动点，PQ⊥AB于点Q，点A的坐标为（0，3）．

(1)、求直线AB的解析式；

(2)、若 $\frac{A Q}{A B} = \frac{4}{5}$ ，求点P的坐标；

(3)、当P在y轴负半轴时，连接BP、OQ，分别取BP、OQ的中点E、F，连接EF交PQ于点G，当OQ $//$ BP时，求证： $P B^{2} = 2 P G \cdot P Q$ ．

查看试题解析