福建省三明市将乐县2020-2021学年八年级上学期数学期中试卷

试卷更新日期：2021-01-06 类型：期中考试

进入出卷网下载

一、单选题

1. 4的算术平方根是（　　）

A、 ±2 B、2 C、﹣2 D、±16

查看试题解析
2. 在平面直角坐标系中，点P（﹣3，﹣4）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 在实数 $\sqrt{2}$ ， $\frac{22}{7}$ ， 0.101001， $\sqrt{4}$ 中，无理数的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
4. 化简 $\sqrt{\frac{3}{8}}$ 得：（）

A、 $\frac{\sqrt{24}}{8}$ B、 $\frac{\sqrt{3}}{4}$ C、 $\frac{\sqrt{6}}{4}$ D、 $\frac{\sqrt{3}}{2 \sqrt{2}}$

查看试题解析
5. 点A₁（5， –7）关于x轴对称的点A₂的坐标为（）

A、（–5, –7） B、（–7 ，–5） C、（5，7） D、（7， –5）

查看试题解析
6. 若点P（x, y）在第二象限，且 $| x | = 2, | y | = 3$ ，则x + y =（）

A、－1 B、1 C、5 D、－5

查看试题解析
7. 已知点M(1，a)和点N(2，b)是一次函数y=－2x＋1图象上的两点，则a与b的大小关系是（）

A、a＞b B、a=b C、a＜b D、以上都不对

查看试题解析
8. 满足下列条件的 $Δ A B C$ 中，不是直角三角形的是 $($ $)$

A、 $b^{2} = c^{2} - a^{2}$ B、 $a ： b ： c = 3 ： 4 ： 5$ C、 $∠ C = ∠ A - ∠ B$ D、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$

查看试题解析
9. 一次函数=kx+b（k≠0）在平面直角坐标系内的图象如图所示，则k和b的取值范围是（）

A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＜0 D、k＜0，b＞0

查看试题解析
10. 如图，在平面直角坐标系中，A（1， 1），B（2， 2），直线 $y = k x + x + 3$ 与线段 $A B$ 有公共点，则k的取值范围是（）

A、 $k \geq - 3$ B、 $k < - \frac{3}{2}$ C、 $- 3 < k < - \frac{3}{2}$ D、 $- 3 \leq k \leq - \frac{3}{2}$

查看试题解析

二、填空题

11. 计算： $(2 \sqrt{3} + 3) (2 \sqrt{3} － 3)$ = ．

查看试题解析
12. 平面直角坐标系内，点P（3，﹣4）到y轴的距离是.

查看试题解析
13. 如图，池塘边有两点A，B，点C是与BA方向成直角的AC方向上的点，测得BC =25m，AC=15m，则A，B两点间的距离是m．

查看试题解析
14. 如图，已知点A的坐标为（−2，2），点C的坐标为（2，1），则点B的坐标是．

查看试题解析
15. 正比例函数y=kx的图象经过点A（2，-3）和B（a，3），则a的值为

查看试题解析
16. 如图，正方形OABC的边长为6，点A、C分别在x轴，y轴的正半轴上，点D（2，0）在OA上，P是OB上一动点，则PA+PD的最小值为.

查看试题解析

三、解答题

17.

(1)、 $\sqrt{25} + \sqrt[3]{- 27} - \sqrt{\frac{1}{9}}$ ；

(2)、 $3 \sqrt{5} (\sqrt{5} - 2) - \frac{\sqrt{6} \times \sqrt{3}}{\sqrt{2}}$ ．

查看试题解析
18. 在如图所示的直角坐标系中．

(1)、描出点A（–3，2）、B（–2，5）、O（0，0），并用线段顺次连接点A、B、O，得 $△ A B O$ ；

(2)、在直角坐标系内画出 $△ A B O$ 关于y轴对称的 $△ A_{1} B_{1} O$ ；

(3)、分别写出点A₁、点B₁的坐标．

查看试题解析
19. 如果一个正数x的两个平方根分别为a＋1和a－5.

(1)、求a和x的值；

(2)、求7x＋1的立方根.

查看试题解析
20. 已知：一次函数y=2x+4．

(1)、在直角坐标系内画出一次函数y=2x+4的图象；

(2)、求图象与x轴和y轴的交点坐标．

查看试题解析
21. 一张直角三角形的纸片，如图所示折叠，使两个锐角的顶点A、B重合，若AC=6cm，AB=10cm，求DC的长．

查看试题解析
22. 如图，△ABC是边长为 6 的等边三角形，在平面直角坐标系中，边AB与 x 轴重合，点C在 x 轴上方， B点的坐标为（9， 0）．

求：

(1)、点A，C 的坐标；

(2)、求△ABC的面积．

查看试题解析
23. 如图，一只蚂蚁沿长方体的表面从顶点A爬到另一顶点M，已知AB =3，AD = 4，BF = 5．求这只蚂蚁爬行的最短距离．

查看试题解析
24. 某机动车出发前油箱内有油42L，行驶若干小时后，途中在加油站加油若干升，油箱中余油量Q（L）与行驶时间t（h）之间的函数关系如图所示，根据图回答问题：

(1)、机动车行驶h后加油；

(2)、加油前油箱余油量Q与行驶时间t的函数关系式是；

(3)、中途加油L；

(4)、如果加油站距目的地还有230km，车速为40km/h，要到达目的地，油箱中的油是否够用？请说明理由．

查看试题解析
25. 如图，直线EF与x轴、y轴分别交于点E（-8，0），F（0，6）．

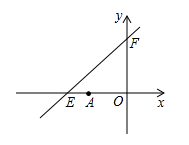(1)、求直线EF的函数表达式；

(2)、若点A的坐标为（-6，0），点P（m，n ）在线段EF上（不与点E重合）
①求△OPA的面积S与m的函数表达式；

②求当△OPA的面积为9时，点P的坐标；

③求当△OPA的面积与△OPF的面积相等时，点P的坐标．

查看试题解析