福建省泉州市惠安县第三教研联盟2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-01-06 类型:期中考试
一、单选题
-
1. 下列实数中,属于无理数的是( )A、3.14 B、 C、 D、2. 下列算式中,结果等于 的是( )A、 B、 C、 D、3. 计算(x-3)(x+2)的结果是( )A、 B、x2-5x+6 C、x2-x-6 D、x2-5x-64. 估算+3的值( )
A、在5和6之间 B、在6和7之间 C、在7和8之间 D、在8和9之间5. 下列从左到右的变形,属于因式分解的是( )A、 B、 C、 D、6. 现规定一种运算: ,其中 , 为实数,则 等于( )A、-2 B、-6 C、2 D、67. 若 的结果不含 的一次项,则 , 应满足( )A、 B、 C、 D、8. 从边长为 的正方形内去掉一个边长为b的小正方形(如图1),然后将剩余部分剪拼成一个矩形(如图2),上述操作所能验证的等式是( )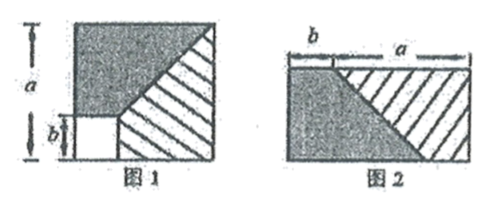 A、 B、 C、 D、9. 已知 则 的大小关系是( )A、 B、 C、 D、10. 有一个数值转换器,流程如下:
A、 B、 C、 D、9. 已知 则 的大小关系是( )A、 B、 C、 D、10. 有一个数值转换器,流程如下:
当输入的 为256时,输出的 是( )
A、 B、 C、 D、二、填空题
-
11. 的平方根是 .12. 比较大小: 3.(填“>”、“=”或“<”)13. 为了使 成为一个整式的完全平方式,加上一个实数为14. 若多项式与单项式 的积是 ,则该多项式为 .15. 若 ,则 .16. 已知 时, .请你根据这个结论直接填空:(1)、 ;(2)、若 ,则
三、解答题
-
17. 计算:(1)、(2)、18. 分解因式:(1)、(2)、19. 先化简,再求值: ,其中x=-2.20. 已知 , .求下列各式的值:(1)、 .(2)、 .21. 已知实数 , 满足 ,(1)、求 , 的值;(2)、求 的平方根.22. 规定两数a、b之间的一种运算,记作(a,b):如果 ,那么(a,b)=c.
例如:因为 ,所以(2,8)=3.
(1)、根据上述规定,填空:(5,125)= , (-2,4)= , (-2,-8)=;
(2)、小明在研究这种运算时发现一个现象: ,他给出了如下的证明:设 ,则 ,即
∴ ,即 ,
∴ .
请你尝试运用上述这种方法说明下面这个等式成立的理由.
(4,5)+(4,6)=(4,30)
23. 如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).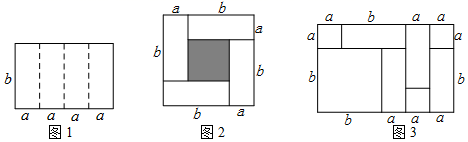 (1)、图2中的阴影部分的面积为 ;(2)、观察图2请你写出(a+b)2、(a-b)2、ab之间的等量关系是 ;(3)、根据(2)中的结论,若x+y=7,xy= ,则x-y= ;(4)、实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等式 .24. 南山植物园中现有A,B两个园区.已知A园区为长方形,长为(x+y)米,宽为(x-y)米;B园区为正方形,边长为(x+3y)米.(1)、请用代数式表示A,B两园区的面积之和并化简.(2)、现根据实际需要对A园区进行整改,长增加(11x-y)米,宽减少(x-2y)米,整改后A园区的长比宽多350米,且整改后两园区的周长之和为980米.
(1)、图2中的阴影部分的面积为 ;(2)、观察图2请你写出(a+b)2、(a-b)2、ab之间的等量关系是 ;(3)、根据(2)中的结论,若x+y=7,xy= ,则x-y= ;(4)、实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等式 .24. 南山植物园中现有A,B两个园区.已知A园区为长方形,长为(x+y)米,宽为(x-y)米;B园区为正方形,边长为(x+3y)米.(1)、请用代数式表示A,B两园区的面积之和并化简.(2)、现根据实际需要对A园区进行整改,长增加(11x-y)米,宽减少(x-2y)米,整改后A园区的长比宽多350米,且整改后两园区的周长之和为980米.①求x,y的值;
②若A园区全部种植C种花,B园区全部种植D种花,且C,D两种花投入的费用与吸引游客的收益如下表:
C
D
投入(元/米2)
12
16
收益(元/米2)
18
26
求整改后A,B两园区旅游的净收益之和.(净收益=收益-投入)
25. 已知 , .设 , , ,…, .(1)、计算 ;(2)、请阅读下面计算 的过程:, ,
.
你读懂了吗?请你先填空完成(2)中 的计算结果,再计算 ;
(3)、猜想并写出 , , 三者之间的数量关系(不要求证明),根据得出的数量关系计算 .