福建省宁德福鼎市2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-01-06 类型:期中考试
一、单选题
-
1. 下列各数中,属于无理数的是( )A、 B、 C、 D、2. 下列各组数为边长的三角形中,能组成直角三角形的是( )A、5,12,13 B、5,6,8 C、6,8,12 D、8,10,123. 在平面直角坐标系中,点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列二次根式中,与 是同类二次根式的是( )A、 B、 C、 D、5. 下列运算中,正确的是( )A、 B、 C、 D、6. 已知关于 的一次函数 的图象经过点A( , ),B( , ),则 , 的大小关系为( )A、 B、 C、 D、7. 数轴上表示下列各数的点,能落在A , B两个点之间的是( )
 A、 B、 C、 D、8. 在平面直角坐标系中,一次函数 的图象是( )A、
A、 B、 C、 D、8. 在平面直角坐标系中,一次函数 的图象是( )A、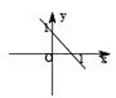 B、
B、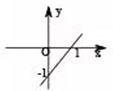 C、
C、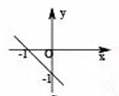 D、
D、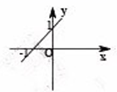 9. 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(单位:km)与甲车行驶时间x(单位:h)之间的函数关系如图所示,根据图象提供的信息,下列结论错误的是( )
9. 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(单位:km)与甲车行驶时间x(单位:h)之间的函数关系如图所示,根据图象提供的信息,下列结论错误的是( ) A、两城相距480千米 B、乙车比甲车晚出发1小时,却早到1小时 C、当乙车到达B城时,甲车距离B城80千米 D、甲车出发后4小时,乙车追上甲车10. 如图,在 中,AB=AC=6,∠B=45°,D是BC上一个动点,连接AD , 以AD为边向右侧作等腰 ,其中AD=AE , ∠ADE=45°,连接CE . 在点D从点B向点C运动过程中, 周长的最小值是( )
A、两城相距480千米 B、乙车比甲车晚出发1小时,却早到1小时 C、当乙车到达B城时,甲车距离B城80千米 D、甲车出发后4小时,乙车追上甲车10. 如图,在 中,AB=AC=6,∠B=45°,D是BC上一个动点,连接AD , 以AD为边向右侧作等腰 ,其中AD=AE , ∠ADE=45°,连接CE . 在点D从点B向点C运动过程中, 周长的最小值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 2的相反数是 .12. 若电影票上座位是12排5号可记为(12,5),则(5,6)表示 .13. 在平面直角坐标系中,点 关于 轴对称的点的坐标是 .14. 在△ABC中,AB=4,AC=3,BC=5,则△ABC的面积是 .15. 如果一个长方形的面积为 ,它的长是 ,那么这个长方形的周长是 .16. 如图,在正方形ABCD中,AB=4,O是AB中点,E是BC上一点,将△OBE沿OE所在直线对折得到△ ,若△ 是以 为腰的等腰三角形,则BE的长为 .

三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子的 ,则梯子比较稳定.现有一长度为6 m的梯子,当梯子稳定摆放时,它的顶端能达到多高?
 19. 在如图所示的平面直角坐标系中,点A , B , C的位置如图所示.
19. 在如图所示的平面直角坐标系中,点A , B , C的位置如图所示. (1)、请写出点A , B , C的坐标;(2)、在坐标系内确定点D , 使得四边形ABCD是正方形,并写出点D的坐标.20. 某水果超市营销员的个人收入与他每月的销售量成一次函数关系,其图象如下,请你根据图象提供的信息,解答以下问题:
(1)、请写出点A , B , C的坐标;(2)、在坐标系内确定点D , 使得四边形ABCD是正方形,并写出点D的坐标.20. 某水果超市营销员的个人收入与他每月的销售量成一次函数关系,其图象如下,请你根据图象提供的信息,解答以下问题: (1)、求营销员的个人收入y(元)与营销员每月销售量x(千克)( )之间的函数关系式;(2)、营销员佳妮想得到收入1600元,她应销售水果多少千克?21. 我们知道无理数 都可以化为无限不循环小数,所以 的小数部分不可能全部写出来,若 的整数部分为a , 小数部分为b , 则 ,且 .(1)、 的整数部分是 , 小数部分是;(2)、若 的整数部分为m , 小数部分为n , 求 的值.22. 意大利著名画家达•芬奇用如图所示的方法证明了勾股定理,其中左图的空白部分是由两个正方形和两个直角三角形组成,右图的空白部分由两个直角三角形和一个正方形组成.设左图中空白部分的面积为S1 , 右图中空白部分的面积为S2 .
(1)、求营销员的个人收入y(元)与营销员每月销售量x(千克)( )之间的函数关系式;(2)、营销员佳妮想得到收入1600元,她应销售水果多少千克?21. 我们知道无理数 都可以化为无限不循环小数,所以 的小数部分不可能全部写出来,若 的整数部分为a , 小数部分为b , 则 ,且 .(1)、 的整数部分是 , 小数部分是;(2)、若 的整数部分为m , 小数部分为n , 求 的值.22. 意大利著名画家达•芬奇用如图所示的方法证明了勾股定理,其中左图的空白部分是由两个正方形和两个直角三角形组成,右图的空白部分由两个直角三角形和一个正方形组成.设左图中空白部分的面积为S1 , 右图中空白部分的面积为S2 . (1)、请用含a , b , c的代数式分别表示S1 , S2;(2)、请利用达•芬奇的方法证明勾股定理.23. 定义:若一个三角形一边上的中线等于该边的长,则称这个三角形为“平等三角形”,这条中线称为该边上的“平等线”.如图1,已知△ABC中,D是BC上一点,连接AD , 若AD平分BC , 且AD=BC , 则△ABC是“平等三角形”,AD是BC边上的“平等线”.
(1)、请用含a , b , c的代数式分别表示S1 , S2;(2)、请利用达•芬奇的方法证明勾股定理.23. 定义:若一个三角形一边上的中线等于该边的长,则称这个三角形为“平等三角形”,这条中线称为该边上的“平等线”.如图1,已知△ABC中,D是BC上一点,连接AD , 若AD平分BC , 且AD=BC , 则△ABC是“平等三角形”,AD是BC边上的“平等线”.

 (1)、如图2,已知△ABC , AB=AC= ,点D是BC的中点,BC=6,判断△ABC是否是“平等三角形”,并说明理由;(2)、如图3,在△ABC中,∠C=90°,AC=8,若△ABC是“平等三角形”,求BC的长.24. 如图,已知点M坐标为(1, ),点N坐标为(0, ).直线 (k ≠ 0)经过点M , 交y轴于点A , 交x轴于点B .
(1)、如图2,已知△ABC , AB=AC= ,点D是BC的中点,BC=6,判断△ABC是否是“平等三角形”,并说明理由;(2)、如图3,在△ABC中,∠C=90°,AC=8,若△ABC是“平等三角形”,求BC的长.24. 如图,已知点M坐标为(1, ),点N坐标为(0, ).直线 (k ≠ 0)经过点M , 交y轴于点A , 交x轴于点B . (1)、用含k的代数式表示b;(2)、当 时,若AM=MN , 求直线 的函数表达式;(3)、直线 ( )经过点N , 若对于任意的实数x都有 成立,求直线 的函数表达式.
(1)、用含k的代数式表示b;(2)、当 时,若AM=MN , 求直线 的函数表达式;(3)、直线 ( )经过点N , 若对于任意的实数x都有 成立,求直线 的函数表达式.