山东省日照市五莲县2020-2021学年高二上学期数学期中考试试卷
试卷更新日期:2021-01-06 类型:期中考试
一、单选题
-
1. 若向量 ,向量 ,且满足向量 ,则 等于( )A、1 B、-1 C、2 D、-22. 点(0,﹣1)到直线 距离的最大值为( )A、1 B、 C、 D、23. 已知向量 为平面 的法向量,点 在 内,则点 到平面 的距离为( )A、 B、 C、 D、4. 古希腊数学家阿基米德利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积.若椭圆 的中心为原点,焦点 , 均在 轴上, 的面积为 ,过点 的直线交 于点 , ,且 的周长为8.则 的标准方程为( )A、 B、 C、 D、5. 在平面内,A,B是两个定点,C是动点,若 ,则点C的轨迹为( )A、圆 B、椭圆 C、抛物线 D、直线6. 如图,正方体 的棱长为 ,对角线 和 相交于点 ,则( ).
 A、 B、 C、 D、7. 台风中心从A地以每小时20km的速度向东北方向移动,离台风中心30km内的地区为危险地区,若城市B在A地正东40km处,则B城市处于危险区内的时间为( )A、0.5h B、1h C、1.5h D、2h8. 已知双曲线 : 的左、右焦点分别为 , ,点P是C的右支上一点,连接 与y轴交于点M,若 (O为坐标原点), ,则双曲线C的渐近线方程为( )A、 B、 C、 D、
A、 B、 C、 D、7. 台风中心从A地以每小时20km的速度向东北方向移动,离台风中心30km内的地区为危险地区,若城市B在A地正东40km处,则B城市处于危险区内的时间为( )A、0.5h B、1h C、1.5h D、2h8. 已知双曲线 : 的左、右焦点分别为 , ,点P是C的右支上一点,连接 与y轴交于点M,若 (O为坐标原点), ,则双曲线C的渐近线方程为( )A、 B、 C、 D、二、多选题
-
9. 已知直线 : .( )A、直线 与直线 平行 B、直线 与直线 平行 C、直线 与直线 垂直 D、直线 与直线 垂直10. 已知曲线 .( )A、若m>n>0,则C是椭圆,其焦点在y轴上 B、若m=n>0,则C是圆,其半径为 C、若mn<0,则C是双曲线,其渐近线方程为 D、若m=0,n>0,则C是两条直线11. 在正方体 中, 分别是 和 的中点,则下列结论正确的是( )A、 //平面 B、 平面 C、 D、点 与点 到平面 的距离相等12. 我们通常称离心率为 的椭圆为“黄金椭圆”.如图,已知椭圆 : , 分别为左、右顶点, , 分别为上、下顶点, , 分别为左、右焦点,P为椭圆上一点,则满足下列条件能使椭圆C为“黄金椭圆”的有( )
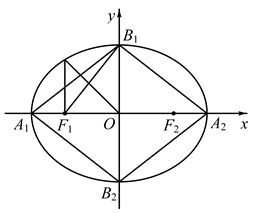 A、 B、 C、 轴,且 D、四边形 的内切圆过焦点 ,
A、 B、 C、 轴,且 D、四边形 的内切圆过焦点 ,三、填空题
-
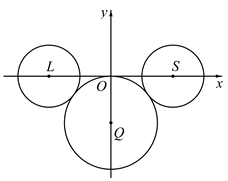
13. 抛物线 的准线方程是 .14. 已知向量 , , ,且 、 、 三点共线,则 = .15. 已知F为双曲线 的右焦点,A为C的右顶点,B为C上的点,且BF垂直于x轴.若AB的斜率为3,则C的离心率为.16. 2020年是中国传统的农历“鼠年”,有人用3个圆构成“卡通鼠”的形象,如图: 是圆Q的圆心,圆Q过坐标原点O;点L、S均在 轴上,圆L与圆S的半径都等于2,圆S、圆L均与圆Q外切.已知直线l过点O.若直线l截圆L、圆S、圆Q所得弦长均等于d,则d= .
四、解答题
-
17. 已知直线 经过两条直线 和 的交点,且与直线 垂直.(1)、求直线 的方程;(2)、若圆 过点 ,且圆心在 轴的正半轴上,直线 被该圆所截得的弦长为 ,求圆 的标准方程.18. 已知长方体 , , , 为棱 的中点, 为线段 的中点.
 (1)、求异面直线 与 所成角的余弦值;(2)、求直线 与平面 所成角的正弦值.19. 已知椭圆C中心在原点,焦点在x轴上,离心率为 ,且一个焦点和短轴的两个端点构成面积为1的等腰直角三角形.(1)、求椭圆的标准方程;(2)、过椭圆C右焦点F作直线交椭圆C于点M,N,又直线 交直线 于点T,若 ,求线段 的长.20. 已知点 , ,曲线 任意一点 满足 .(1)、求曲线 的方程;(2)、设点 ,问是否存在过定点 的直线 与曲线 相交于不同两点 ,无论直线 如何运动, 轴都平分 ,若存在,求出 点坐标,若不存在,请说明理由.
(1)、求异面直线 与 所成角的余弦值;(2)、求直线 与平面 所成角的正弦值.19. 已知椭圆C中心在原点,焦点在x轴上,离心率为 ,且一个焦点和短轴的两个端点构成面积为1的等腰直角三角形.(1)、求椭圆的标准方程;(2)、过椭圆C右焦点F作直线交椭圆C于点M,N,又直线 交直线 于点T,若 ,求线段 的长.20. 已知点 , ,曲线 任意一点 满足 .(1)、求曲线 的方程;(2)、设点 ,问是否存在过定点 的直线 与曲线 相交于不同两点 ,无论直线 如何运动, 轴都平分 ,若存在,求出 点坐标,若不存在,请说明理由.

