初中数学北师大版九年级下学期 第二章 单元测试卷
试卷更新日期:2021-01-06 类型:单元试卷
一、单选题
-
1. 下列函数中是二次函数的是( )A、 B、 C、 D、2. 二次函数 的顶点坐标是( )A、 B、 C、 D、3. 将抛物线y=﹣(x+1)2+3向右平移2个单位再向上平移2个单位后得到的新抛物线的表达式为( )A、y=﹣(x+3)2+1 B、y=﹣(x﹣1)2+5 C、y=﹣(x+1)2+5 D、y=﹣(x+3)2+54. 二次函数 的图像一定经过( )A、第一、二象限 B、第三、四象限 C、第一、三象限 D、第二、四象限5. 二次函数 的图象经过点(0,2),则a+b的值是( )A、-3 B、-1 C、2 D、36. 将抛物线C:y=x2+3x-10平移到C′.若两条抛物线C,C′关于直线x=1对称,则下列平移方法中正确的是( )A、将抛物线C向右平移 个单位 B、将抛物线C向右平移3个单位 C、将抛物线C向右平移5个单位 D、将抛物线C向右平移6个单位7. 已知 , 是函数 上的点,则( ).A、 B、 C、 D、 , 的大小关系不确定8. 对于抛物线y=-2(x+1)2+3,下列结论:
①抛物线的开口向下②对称轴为直线x=1
③顶点坐标为(1,3)④x>1时,y随x的增大而减小
其中正确结论的个数为( )
A、1 B、2 C、3 D、49. 二次函数y=ax2+bx+c的图象如下左图所示,则一次函数y=ax+b和反比例函数y 在同一平面直角坐标系中的图象可能是( ) A、
A、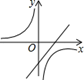 B、
B、 C、
C、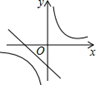 D、
D、 10. 如图,是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A , B两点,下列结论:①2a+b=0;m+n=3;②抛物线与x轴的另一个交点是(﹣1,0);③方程ax2+bx+c=3有两个相等的实数根;④当1 x 4时,有y2 y1;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=1.正确的为( )
10. 如图,是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A , B两点,下列结论:①2a+b=0;m+n=3;②抛物线与x轴的另一个交点是(﹣1,0);③方程ax2+bx+c=3有两个相等的实数根;④当1 x 4时,有y2 y1;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=1.正确的为( )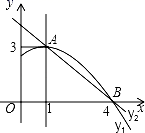 A、①④⑤ B、①③④ C、①③⑤ D、①②③
A、①④⑤ B、①③④ C、①③⑤ D、①②③二、填空题
-
11. 抛物线 向右平移2个单位,得到新的抛物线的解析式是.12. 二次函数y=-x2﹣4x的最高点的坐标是.13. 抛物线 的对称轴是.14. 如果抛物线 有最低点,那么 的取值范围是 .15. 如图,抛物线 = 与直线 = 相交于点 , ,则关于 的方程 = 的解为 .
 16. 如图,抛物线 与 交于点 ,过点 作 轴的平行线,分别交两条抛物线于点 , .则以下结论:①无论 取何值, 2的值总是正数;② ;③当 时, ;④ .其中正确结论是 .
16. 如图,抛物线 与 交于点 ,过点 作 轴的平行线,分别交两条抛物线于点 , .则以下结论:①无论 取何值, 2的值总是正数;② ;③当 时, ;④ .其中正确结论是 .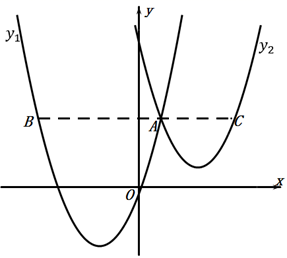
三、解答题
-
17. 若二次函数y=ax2+bx+c的图象的顶点是(2,1)且经过点(1,2),求此二次函数解析式.18. 二次函数y=a(x-h)2的图象如图,已知a= ,OA=OC,试求该抛物线的解析式.
 19. 已知二次函数 的图象与 轴交于A、B两点,且经过C(1,-2),求点A、B的坐标和 的值.20. 某商店的一种服装,每件成本为50元.经市场调研,售价为60元时,可销售200件,售价每提高1元,销售量将减少10件.那么,该服装每件售价是多少元时,商店销售这批服装获利能达到2240元?21. 如图,已知在平面直角坐标系中,抛物线过点 , , .求抛物线的解析式,并求出抛物线的顶点 的坐标.
19. 已知二次函数 的图象与 轴交于A、B两点,且经过C(1,-2),求点A、B的坐标和 的值.20. 某商店的一种服装,每件成本为50元.经市场调研,售价为60元时,可销售200件,售价每提高1元,销售量将减少10件.那么,该服装每件售价是多少元时,商店销售这批服装获利能达到2240元?21. 如图,已知在平面直角坐标系中,抛物线过点 , , .求抛物线的解析式,并求出抛物线的顶点 的坐标. 22. 如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
22. 如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D. (1)、求二次函数的表达式;(2)、在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;(3)、有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从 点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M,N同时停止运动,问点M,N运动到何处时,△MNB面积最大,试求出最大面积.
(1)、求二次函数的表达式;(2)、在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;(3)、有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从 点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M,N同时停止运动,问点M,N运动到何处时,△MNB面积最大,试求出最大面积.