初中数学北师大版九年级下学期第二章 2.3 确定二次函数的表达式

试卷更新日期：2021-01-06 类型：同步测试

进入出卷网下载

1. 已知二次函数y=mx²+x+m（m-2）的图像经过原点，则m的值为（）

A、0或2 B、0 C、2 D、无法确定

查看试题解析
2. 抛物线y＝ax²+bx﹣3与x轴交于A ， B两点，与y轴交于点C ，且OB＝OC＝3OA ，求抛物线的解析式（）

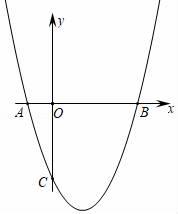A、y＝x²﹣2x﹣3 B、y＝x²﹣2x+3 C、y＝x²﹣2x﹣4 D、y＝x²﹣2x﹣5

查看试题解析
3. 已知二次函数的图象如图所示，则这个二次函数的表达式为（）

A、 $y = x^{2} - 2 x + 3$ B、 $y = x^{2} - 2 x - 3$ C、 $y = x^{2} + 2 x - 3$ D、 $y = x^{2} + 2 x + 3$

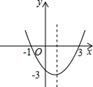查看试题解析
4. 二次函数y=x²+bx+c，经过配方可化为y=(x-1)²+2，则b，c的值分别为（）

A、5，-1 B、-2，3 C、-2，-3 D、2，3

查看试题解析
5. 如图为抛物线 $y = a x^{2} + b x + c$ 的图像，A，B，C 为抛物线与坐标轴的交点，且OA=OC=1，则下列关系中正确的是（）

A、a＋b=－1 B、a－b=－1 C、b<2a D、ac<0

查看试题解析
6. 二次函数的部分图象如图所示，对称轴是x=﹣1，则这个二次函数的表达式为（）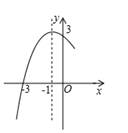

A、y=﹣x²+2x+3 B、y=x²+2x+3 C、y=﹣x²﹣2x+3 D、y=﹣x²+2x﹣3

查看试题解析

7. 将二次函数y=x²-2x+3化为y=（x-h）²+k的形式，则h= ， k= ．

查看试题解析
8. 如图，已知抛物线y=﹣x²+bx+c的对称轴为直线x=1，且与x轴的一个交点为（3，0），那么它对应的函数解析式是.

查看试题解析
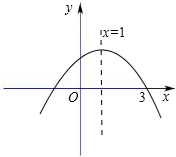9. 已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 图象的顶点为 $P (- 2, 3)$ ，且过 $A (- 3, 0)$ ，则抛物线的关系式为．

查看试题解析
10. 抛物线y=ax²+bx+c经过A（﹣2，4），B（6，4）两点，且顶点在x轴上，则该抛物线解析式为．

查看试题解析
11. 如果抛物线 $y = - x^{2} + 3 x - 1 + m$ 经过原点，那么m=.

查看试题解析
12. 二次函数 $y = - x^{2} + 2 x + 3$ 的图象与 $x$ 轴交于 $A$ 、 $B$ 两点， $P$ 为它的顶点，则 $S_{△ P A B} =$ ．

查看试题解析

13.
用配方法把下列二次函数化成顶点式： $y = \frac{1}{2} x^{2} + 2 x + 5$ ．

查看试题解析
14. 二次函数y＝ax²+bx+c（a≠0）的图象过点A（﹣1，8）、B（2，﹣1），与y轴交于点C（0，3），求二次函数的表达式．

查看试题解析
15. 已知抛物线的顶点坐标 $(1, 2)$ 且过点 $(3, 0)$ ，求该抛物线的解析式．

查看试题解析
16. 如图，已知点 $A (0 ， 2)$ ，点 $B (4 ， 2)$ ，抛物线 $y = - \frac{1}{2} {(x - h)}^{2} + k$ (h ， k均为常数)与线段AB交于C ， D两点，且 $C D = \frac{1}{2} A B$ ，求k的值．

查看试题解析

初中数学北师大版九年级下学期 第二章 2.3 确定二次函数的表达式