浙江省金华市2020-2021学年七年级上学期数学期末模拟试卷

试卷更新日期：2021-01-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各对数中，互为相反数的是（）

A、-（-2）和2 B、+（-3）和-（+3） C、 $\frac{1}{2}$ 和-2 D、-(-5）和-|-5|

查看试题解析
2. “扶贫”是新时期党和国家的重点工作之一，为落实习近平总书记提出的“精准扶贫”战略构想，某省预计三年内脱贫1020000人，数字1020000用科学记数法可表示为（）

A、1.02×10⁶ B、1.02×10⁵ C、10.2×10⁵ D、102×10⁴

查看试题解析
3. 若 $a = - {(- 2)}^{2}$ ， $b = - {(- 3)}^{3}$ ， $c = - (- 4^{2})$ ，则 $- [a - (b - c)]$ 的值是（）

A、15 B、7 C、 $- 39$ D、17

查看试题解析
4. 下列运算正确的是（）

A、 ${(- 1)}^{2020} = - 1$ B、 $- 2^{2} = 4$ C、 $\sqrt{9} = \pm 3$ D、 $\sqrt[3]{- 27} = - 3$

查看试题解析
5. 如图，点 $C ， D$ 在线段 $A B$ 上， $A C = \frac{1}{3} C B$ ，点 $D$ 是 $C B$ 的中点，若 $C D = 6$ ，则 $A B$ 等于（）

A、 $16$ B、 $18$ C、 $20$ D、 $22$

查看试题解析
6. 若 ${(x + 1)}^{2} + | y - 2 | = 0$ ，则 $x^{2} - y =$ （）

A、-3 B、0 C、3 D、-1

查看试题解析
7. 下列一组数：﹣8；2.7； $- 3 \frac{1}{2}$ ； $\frac{π}{2}$ ；0.66666…；0；2；0.080080008…（相邻两个8之间依次增加一个0）其中是无理数的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 如图，直线 $A B$ 与直线 $C D$ 交于点O， $O E ⊥ A B$ ， $O F$ 平分 $∠ A O C$ ，若 $∠ B O D = 70^{°}$ ．则 $∠ E O F$ 的度数为（）

A、115° B、145° C、135° D、125°

查看试题解析
9. 西安某厂车间原计划15小时生产一批急用零件，实际每小时多生产了10个，用了12小时不但完成了任务，而且还多生产了30个.设原计划每小时生产x个零件，则所列方程为（）

A、 $\frac{x}{15} - \frac{x + 30}{12} = 10$ B、 $\frac{x + 30}{12} - \frac{x}{15} = 10$ C、 $12 (x + 10) = 15 x + 30$ D、 $15 x = 12 (x + 10) + 30$

查看试题解析
10. 按照如图所示的计算机程序计算，若开始输入的x值为2，第一次得到的结果为1，第二次得到的结果为4，…第2018次得到的结果为（）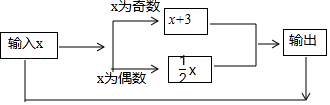

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 一个数的平方等于64，则这个数为．

查看试题解析
12. $- \frac{x y^{2}}{6}$ 的系数为，次数为．

查看试题解析
13. 关于x的方程 $x - a = 7$ 的解是 $x = 2$ ，则a的值为．

查看试题解析
14. 已知当 $x = 1$ 时， $2 a x^{2} - b x$ 的值为 $- 3$ ，则当 $x = 2$ 时，代数式 $a x^{2} - b x$ 的值是．

查看试题解析
15. 点 $A, B, C$ 在同一条数轴上，且点 $A$ 表示的数为－1，点 $B$ 表示的数为5.若 $B C = 2 A C$ ，则点 $C$ 表示的数为.

查看试题解析
16. 如图，已知点A、点B是直线上的两点，AB=12厘米，点C在线段AB上，且BC=4厘米．点P、点Q是直线上的两个动点，点P的速度为1厘米/秒，点Q的速度为2厘米/秒．点P、Q分别从点C、点B同时出发在直线上运动，则经过秒时线段PQ的长为5厘米．

查看试题解析

三、综合题

17. 计算:

(1)、 $(- 81) \div 2 \frac{1}{4} \times \frac{4}{9} \div (- 16)$ ；

(2)、 ${(- 4)}^{2} - 3^{3} \times {(- \frac{1}{3})}^{2}$ ．

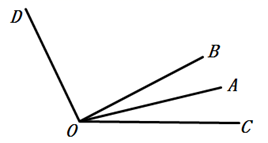
查看试题解析
18. 化简

(1)、－2a²b＋3ab²－2ab²＋3a²b

(2)、 $3 (2 x^{2} - x + 1) - 2 (1 - 3 x^{2})$

查看试题解析
19. 先化简，再求值： $- \frac{1}{2} (x y - x^{2}) + 3 (y^{2} - \frac{1}{2} x^{2}) + 2 (\frac{1}{4} x y - \frac{1}{2} y^{2})$ ，其中 $x = 2, y = \frac{1}{2}$ ．

查看试题解析
20. 解方程

(1)、 $2 x = 9 - x$ ；

(2)、 $\frac{2 x + 1}{3} - \frac{5 x - 1}{6} = 1$ .

查看试题解析
21. 如图∠COD=116°，∠BOD=90°，OA平分∠BOC，求∠AOD的度数．

查看试题解析
22. 某工厂第一车间有x人，第二车间比第一车间人数的 $\frac{4}{5}$ 少30人，如果从第二车间调出10人到第一车间。求：

(1)、两个车间共有多少人？

(2)、调动后，第一车间的人数比第二车间多多少人？

查看试题解析
23. 如图所示，在数轴上点A，B，C表示的数分别为﹣2，0，6．点A与点B之间的距离表示为AB，点B与点C之间的距离表示为BC，点A与点C之间的距离表示为AC．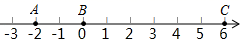

(1)、AB＝， BC＝， AC＝；

(2)、点A，B，C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动．
①设运动时间为t，请用含有t的算式分别表示出AB，BC，AC；

②在①的条件下，请问：BC﹣AB的值是否随着运动时间t的变化而变化？若变化，请说明理由：若不变，请求其值．

查看试题解析
24. 甲、乙两家商场以同样的价格出售同样的电器，但各自推出的优惠方案不同，甲商场规定：凡超过 $1000$ 元的电器，超出的金额按 $80 %$ 收取；乙商场规定：凡超过 $800$ 元的电器，超出的金额按 $90 %$ 收取，某顾客购买的电器价格是 $x$ 元.

(1)、当 $x > 1000$ 时，分别用代数式表示在两家商场购买电器所需付的费用

(2)、当 $x = 1500$ 时，该顾客应选择哪一家商场购买比较合算？说明理由.

查看试题解析