浙江省杭州市2020-2021学年七年级上学期数学期末模拟试卷

试卷更新日期：2021-01-06 类型：期末考试

进入出卷网下载

一、单选题

1. 中国倡导的“一带一路”是中国与世界的互利共赢之路，据统计，“一带一路”地区覆盖的总人口约为44亿人，则“44亿”这个数用科学记数法可表示为（）

A、4.4×10⁷ B、4.4×10⁸ C、4.4×10⁹ D、0.44×10¹⁰

查看试题解析
2. 某同学用剪刀沿直线将一片平整的银杏叶减掉一部分（如图），发现剩下的银杏叶的周长比原银杏叶的周长要小，能符合题意解释这一现象的数学知识是（）

A、两点之间线段最短 B、两点确定一条直线 C、线段的定义 D、圆弧的定义

查看试题解析
3. 下列各式中运算正确的是（）

A、 $2 a - a = 2$ B、 $2 a + 3 b = 5 a b$ C、 $a^{2} + a^{2} = a^{4}$ D、 $6 a^{2} b - 4 a^{2} b = 2 a^{2} b$

查看试题解析
4. 已知有理数a、b在数轴上如图所示，则下列式子错误的是（）

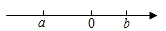A、a＜b B、a＜0 C、|a|＞|b| D、b＜0＜a

查看试题解析
5. 方程 $2 x - 5 = 3 x$ 移项正确的是（）

A、 $2 x + 3 x = 5$ B、 $2 x + 3 x = - 5$ C、 $2 x - 3 x = 5$ D、 $2 x - 3 x = 5$

查看试题解析
6. 如图，B是线段AD的中点，C是线段BD上一点，则下列结论中错误的是（　　）

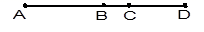A、BC=AB-CD B、BC= $\frac{1}{2}$ (AD-CD) C、BC= $\frac{1}{2}$ AD-CD D、BC=AC-BD

查看试题解析
7. 小幸学习了在数轴上画出表示无理数的点的方法后，进行以下练习：首先画出数轴，原点为O，在数轴上找到表示数2的点A，然后过点A作AB⊥OA，使AB＝3．以点O为圆心，OB为半径作弧，交数轴正半轴于点P，则点P所表示的数介于（　　）

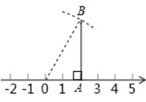A、3和3.5之间 B、3.5和4之间 C、4和4.5之间 D、4.5和5之间

查看试题解析
8. 下列各式计算正确的是（）

A、 $- 12 x y + 7 y x = - 5 x y$ B、 $- 9 \div 2 \times \frac{1}{2} = - 9$ C、 $12 \div (\frac{1}{3} - \frac{1}{2}) = - 2$ D、 $3 a - 4 a = - 1$

查看试题解析
9. 用白铁皮做罐头盒，每张铁皮可制盒身15个或盒底42个，一个盒身与两个盒底配成一套罐头盒. 现有108张白铁皮，用多少张制盒身，多少张制盒底，可以正好制成整套罐头盒？设用 $x$ 张白铁皮制盒身，可列出方程（）

A、 $15 (108 - x) = 2 \times 42 x$ B、 $15 x = 2 \times 42 \times (108 - x)$ C、 $2 \times 15 (108 - x) = 42 x$ D、 $2 \times 15 x = 42 \times (108 - x)$

查看试题解析
10. 如图，在△ABC中，AB=20cm，AC=12 cm，点P从点B出发以每秒3 cm的速度向点A运动，点Q从点A同时出发以每秒2 cm的速度向点C运动，其中一个动点到达端点时，另一个动点也随之停止运动，当∠APQ=∠AQP时，P，Q运动的时间为（）

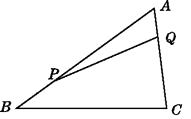A、3秒 B、4秒 C、4.5秒 D、5秒

查看试题解析

二、填空题

11. 单项式 $- \frac{2 a b^{2}}{3}$ 的系数是．

查看试题解析
12. 若 $x = 1$ 是方程 $2 x + a = 0$ 的根，则a= ．

查看试题解析
13. 如图， $∠ 1 = 28^{°} ， A B ⊥ C D ，$ 垂足为O， $E F$ 经过点O．则 $∠ 2$ 的度数是．

查看试题解析
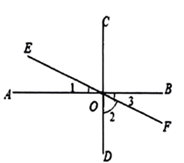14. 有三个互不相等的整数a、b、c，如果abc=9,那么a+b+c= ．

查看试题解析
15. 若x,y为实数，且 $| x - 2 | + {(y + 4)}^{2} = 0,$ 则xy的立方根为。

查看试题解析
16. 规定：[x]表示不大于x的最大整数，（x）表示不小于x的最小整数，[x）表示最接近x的整数（x≠n+0.5，n为整数），例如：[2.3]＝2，（2.3）＝3，[2.3）＝2.当﹣1＜x≤0时，化简[x]+（x）+[x）的结果是.

查看试题解析

三、综合题

17. 计算：

(1)、 $(\frac{1}{3} - \frac{1}{6}) \times (- 24)$

(2)、 $- 1^{4} - (1 - 0.5) \times \frac{1}{3} \times [1 - {(- 2)}^{2}]$ ．

查看试题解析
18. 根据下列语句，画出图形.
如图，已知平面内有四个点 $A$ 、 $B$ 、 $C$ 、 $D$ ，共中任意三点都不在同一直线上.

①画直线 $B C$ ；

②连接 $A C$ 、 $B D$ ，相交于点 $E$ ；

③画射线 $B A$ 、 $C D$ ，交于点 $F$ ；

④过点 $F$ 作 $A C$ 所在直线的垂线段，垂足为点 $G$

查看试题解析
19. 解方程：

(1)、 $17 - 2 x = x - 1$ ；

(2)、 $\frac{x + 1}{2} - \frac{2 - 3 x}{6} = - 1$

查看试题解析
20. 计算：

(1)、 $\sqrt{{(- 5)}^{2}} - | 2 - \sqrt{2} | - \sqrt[3]{- 27}$

(2)、 $\sqrt[3]{0.216} - \sqrt{1 \frac{9}{16}} + 5 \sqrt{\frac{1}{100}}$

查看试题解析
21. 如图，直线 $A B ， C D$ 相交于点 $O ， O D$ 平分 $∠ B O E ， O F$ 平分 $∠ A O E$

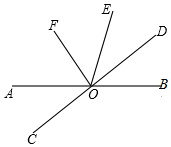(1)、若 $∠ B O E = 58^{°} ， ∠ A O E = 122^{°}$ ，判断 $O F$ 与 $O D$ 的位置关系，并进行证明．

(2)、若 $∠ A O C ： ∠ A O D = 1 ： 5 ，$ 求 $∠ E O F$ 的度数．

查看试题解析
22. 对于题目：“已知 $x^{2} - 2 x - 1 = 0$ ，求代数式 $3 x^{2} - 6 x + 2020$ 的值”，采用“整体代入”的方法（换元法），可以比较容易的求出结果.

(1)、设 $x^{2} - 2 x = y$ ，则 $3 x^{2} - 6 x + 2020 =$ （用含 $y$ 的代数式表示）；

(2)、根据 $x^{2} - 2 x - 1 = 0$ ，得到 $y = 1$ ，所以 $3 x^{2} - 6 x + 2020$ 的值为；

(3)、用“整体代入”的方法（换元法），解决下面问题：
已知 $a + \frac{1}{a} - 5 = 0$ ，求代数式 $\frac{a^{2} - 4 a + 1}{a}$ 的值.

查看试题解析
23. 如图所示，在数轴上点 $A$ ， $B$ ， $C$ 表示的数分别为 $- 2$ ，0，6．点 $A$ 与点 $B$ 之间的距离表示为 $A B$ ，点 $B$ 与点 $C$ 之间的距离表示为 $B C$ ，点 $A$ 与点 $C$ 之间的距离表示为 $A C$ ．

(1)、 $A B =$ ， $B C =$ ， $A C =$ ；

(2)、点 $A$ ， $B$ ， $C$ 开始在数轴上运动，若点 $A$ 以每秒1个单位长度的速度向左运动，同时点 $B$ 和点 $C$ 分别以每秒2个单位长度和5个单位长度的速度向右运动．
①设运动时间为 $t$ ，请用含有 $t$ 的算式分别表示出 $A B$ ， $B C$ ， $A C$ ；
②在①的条件下，请问： $B C - A B$ 的值是否随着运动时间 $t$ 的变化而变化？若变化，请说明理由；若不变，请求其值．

查看试题解析