浙江省湖州市2020-2021学年七年级上学期数学期末模拟试卷
试卷更新日期:2021-01-06 类型:期末考试
一、单选题
-
1. -4的相反数是( ).A、 B、4 C、 D、2. 长虹卧波碧海上,泽被后世万年长.2018年10月24日,我国又一项世界级工程﹣﹣港珠澳大桥正式建成通车.大桥主体工程及三地口岸、连接线共投资约1200亿元.用科学记数法表示1200亿元为( )元.A、1.2×1011 B、12×1011 C、1.2×108 D、1.2×1033. 一副三角板按如图方式摆放,且∠1的度数比∠2的度数大54°,则∠2=( )
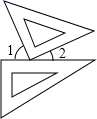 A、18° B、54° C、72° D、70°4. 下列说法中,正确的是( )A、单项式 的系数 B、单项式 的次数为-5 C、多项式 是二次三项式 D、多项式 的常数项是15. 已知 , ,且 .则 的值为( )A、4 B、-4 C、4或-4 D、2或-26. 把方程 的分母化为整数,正确的是( )A、 B、 C、 D、7. 已知代数式 的值为 ,则 的值为( )A、 B、 C、 D、8. 如图,若数轴上 , 两点分别对应有理数 , ,则下列结论正确的是( )
A、18° B、54° C、72° D、70°4. 下列说法中,正确的是( )A、单项式 的系数 B、单项式 的次数为-5 C、多项式 是二次三项式 D、多项式 的常数项是15. 已知 , ,且 .则 的值为( )A、4 B、-4 C、4或-4 D、2或-26. 把方程 的分母化为整数,正确的是( )A、 B、 C、 D、7. 已知代数式 的值为 ,则 的值为( )A、 B、 C、 D、8. 如图,若数轴上 , 两点分别对应有理数 , ,则下列结论正确的是( ) A、 B、 C、 D、 >9. 如图,学校实验室需要向某工厂定制一批三条腿的桌子,已知该工厂有24名工人,每人每天可以生产20块桌面或300条桌腿,1块桌面需要配3条桌腿,为使每天生产的桌面和桌腿刚好配套,设安排 名工人生产桌面,则下面所列方程正确的是( )
A、 B、 C、 D、 >9. 如图,学校实验室需要向某工厂定制一批三条腿的桌子,已知该工厂有24名工人,每人每天可以生产20块桌面或300条桌腿,1块桌面需要配3条桌腿,为使每天生产的桌面和桌腿刚好配套,设安排 名工人生产桌面,则下面所列方程正确的是( ) A、 B、300 C、 D、10. A、B两地相距900千米,甲乙两车分别从A、B两地同时出发,相向而行,已知甲车的速度为110千米/时,乙车的速度为90千米/时,则当两车相距100千米时,甲车行驶的时间是( )
A、 B、300 C、 D、10. A、B两地相距900千米,甲乙两车分别从A、B两地同时出发,相向而行,已知甲车的速度为110千米/时,乙车的速度为90千米/时,则当两车相距100千米时,甲车行驶的时间是( )
A、4小时 B、4.5小时 C、5小时 D、4小时或5小时二、填空题
-
11. 若 元表示收入5元,则支出3元记作元.12. 化简:13. 如图,两条直线AB,CD交于点O,射线OM是∠AOC的平分线,若∠BOD=80°,则∠BOM的度数是.
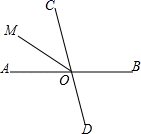 14. 已知7xmy3和- x2yn是同类项,则-nm= .15. 已知a是整数,且a比0大,比10小,请你设法找出a的一些数值,使关于x的方程1﹣ ax=﹣5的解是偶数,你找出的整数a的值是16. ∠A=65º,∠B=75º,将纸片一角折叠,使点C落在△ABC外,若∠2=20º,则∠1的度数为 .
14. 已知7xmy3和- x2yn是同类项,则-nm= .15. 已知a是整数,且a比0大,比10小,请你设法找出a的一些数值,使关于x的方程1﹣ ax=﹣5的解是偶数,你找出的整数a的值是16. ∠A=65º,∠B=75º,将纸片一角折叠,使点C落在△ABC外,若∠2=20º,则∠1的度数为 .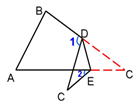
三、综合题
-
17. 计算下列各题:(1)、(2)、18. 如图,已知直线 和直线外三点 , , ,按下列要求画图:
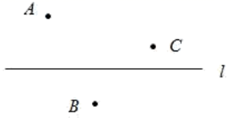
( 1 )画射线 ,画直线 ;
( 2 )画点 到直线 的垂线段,垂足为 ;
( 3 )在直线 上确定点 ,使得 最小,并说明理由.
19. 先简化,再求值: ,其中 ,20. 如图,线段AC=8cm,线段BC=18cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.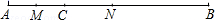 21. 有一种“24点”游戏,其游戏规则是:任取1~13之间的4个自然数,将这4个数(每个数要用且只能用一次)进行加减乘除四则运算,使运算结果为24,例如,对1,2,3,4可作运算:(1+2+3)×4=24[注意上述运算与4×(2+3+1)应视作相同方法的运算].现有数3,4,-6,10,请运用上述规则,写出三种运算式子,使其结果等于24.并选一种写出计算步骤.22. 如图, 平分 , ,已知 ,求 的度数.
21. 有一种“24点”游戏,其游戏规则是:任取1~13之间的4个自然数,将这4个数(每个数要用且只能用一次)进行加减乘除四则运算,使运算结果为24,例如,对1,2,3,4可作运算:(1+2+3)×4=24[注意上述运算与4×(2+3+1)应视作相同方法的运算].现有数3,4,-6,10,请运用上述规则,写出三种运算式子,使其结果等于24.并选一种写出计算步骤.22. 如图, 平分 , ,已知 ,求 的度数.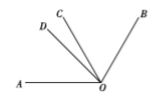 23. 目前全国提倡环保,节能灯在城市已基本普及,某商场计划购进甲、乙两种节能灯共1000只,这两种节能灯的进价,售价如下表:
23. 目前全国提倡环保,节能灯在城市已基本普及,某商场计划购进甲、乙两种节能灯共1000只,这两种节能灯的进价,售价如下表:进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)、如何进货,进货款恰好为37000元?(2)、为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请问乙型节能灯需打几折?24. 已知数轴上三点M,O,N对应的数分别为 ,0,2,点P为数轴上任意一点,其对应的数为x.(1)、如果点P到点M,点N的距离相等,那么x的值是;(2)、数轴上是否存在点P,使点P到点M,点N的距离之和是7?若存在,请直接写出x的值,若不存在,请说明理由;
(3)、如果点P以每分钟3各单位长度的速度从点O向左运动时,点M和点N分别以每分钟1个单位长度和每分钟4个单位长度的速度也向左运动,且三点同时出发,那么几分钟时点P到点M,点N的距离相等.